Page 112 - 201805

694 2018 年 9 月

p t z p t
x
M 0
O d w 
L
M 1 w 
l 2
M 2 d w 2 t
w 2
M 1 L d
l 
M 0
a
p r p r
p i p i
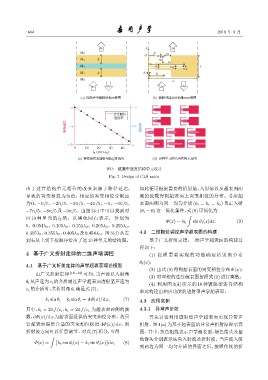
(a) ေਇܦߦ᪔ᒛፇ౞ᇨਓڏ (b) ᪔ᒛیᤚࠍፇ౞ӭЋᇨਓڏ
0 1.0
ቊԫᄱͯ
ᤩ࠱ဋ
ቊԫᄱͯ -p 0.5 ᤩ࠱ဋ

-2p 0
0 10 20 30 40
l 2 (0.01λ 0 )
(c) ቊԫᄱͯԣᤩ࠱ဋᬤl 2 ԫӑڏ (d) 10መӭЋᄊї͵ፇ౞ᇨਓڏ
图 3 镀膜型迷宫结构单元设计
Fig. 3 Design of CLS units

由于迷宫结构单元相位的改变来源于路径延迟， 如此便可根据需要的折射角、入射角以及超表面两
导致的突变相位为负值，相应的突变相位分别应 侧的波数得到超表面上突变相位的分布。考虑超
为 0、−π/5、−2π/5、−3π/5、−4π/5、−π、−6π/5、 表面两侧为同一均匀介质 (k i = k t = k 0 ) 且正入射
−7π/5、−8π/5 及 −9π/5。由图 3(c) 中可以找到对 (θ i = 0)这一简化条件，式(8)可简化为
应 10 种单元的 l 2 值，以黑色圆点表示，分别为 ∫
Φ(x) = k 0 sin θ t (x)dx. (9)
0、0.054λ 0 、0.105λ 0 、0.155λ 0 、0.205λ 0 、0.255λ 0 、
0.305λ 0 、0.355λ 0 、0.405λ 0 及 0.454λ 0 。图 3(d) 从左 4.2 二维相位调控声学超表面的构建
到右从上到下按顺序给出了这10种单元的结构图。 基于广义折射定律，二维声学超表面的构建过
程如下：
4 基于广义折射定律的二维声场调控 (1) 按照需要实现的功能确定折射角分布

θ t (x)；
4.1 基于广义折射定律的声学超表面理论模型
(2) 由式(9)得到超表面的突变相位分布Φ (x)；
由广义折射定律 [18−19] 可知，当声波以入射角
(3) 对理想的连续超表面按照式(1)进行离散；
θ i 从声速为 c i 的介质通过声学超表面透射至声速为
(4) 利用图 3(d) 所示的 10 种镀膜型迷宫结构
c t 的介质时，其折射角θ t 满足式(7)：
单元构建出相应功能的透射型声学超表面。
k t sin θ t − k i sin θ i = dΦ(x)/dx, (7) 4.3 应用实例

其中，k i = 2πf/c i 、k t = 2πf/c t 为超表面两侧的波 4.3.1 异常声折射
数，dΦ(x)/dx 为超表面提供的突变相位分布。故只 首先讨论利用透射型声学超表面实现异常声
要超表面提供合适的突变相位梯度 dΦ(x)/dx，则 折射。图4(a)为基于超表面的异常声折射原理示意
折射波方向可以任意调节。对式(7)积分，可得 图。其中，灰色粗线表示声学超表面，绿色箭头及蓝
∫
[ ] 色箭头分别表示法向入射波及折射波。当声波入射
Φ(x) = k t sin θ t (x) − k i sin θ i (x) dx, (8)
到两边为同一均匀介质的界面之后，按照传统的折