Page 14 - 201903

296 2019 年 5 月

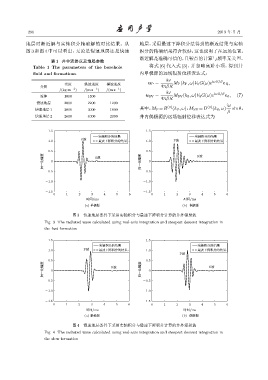
地层时渐近解与实轴积分精确解的对比结果。从 地层，采用最速下降积分法得到的渐近结果与实轴
图 3 和图 4 中可以看出，无论是慢速地层还是快速 积分的精确结果符合较好，这也说明了在远场位置，
渐近解是准确可信的，且鞍点的计算与频率无关 [6] 。
表 1 井中流体以及地层参数
Table 1 The parameters of the borehole 将式 (6) 代入式 (3)，并忽略高阶小项，得到井
fluid and formations 内单极源的远场辐射位移表达式：
−iω iωR/β
密度 纵波速度 横波速度 u P = M P (k P , ω)V 0 G(ω)e e R ,
介质 4πβR
/(kg·m −3 ) /(m·s −1 ) /(m·s −1 )
−iω iωR/β
流体 1000 1500 u SV = M SV (k S , ω)V 0 G(ω)e e θ , (7)
4πβR
慢速地层 2000 2200 1200 iω
快速地层 1 2000 3000 1800 其中，M P =B (0) (k P , ω)，M SV =D (0) (k S , ω) sin θ。
β
快速地层 2 2600 4000 2300 井内偶极源的远场辐射位移表达式为

1.5 1.5
ࠄᣉሥѬᄊፇ౧ ࠄᣉሥѬᄊፇ౧
Pฉ
1.0 తᤴʾᬌሥѬᄊፇ౧ 1.0 Pฉ తᤴʾᬌሥѬᄊፇ౧
0.5 0.5 Sฉ
ॆʷӑࣨए 0 Sฉ ॆʷӑࣨए 0

-0.5 -0.5

-1.0 -1.0

-1.5 -1.5
0 1 2 3 4 5 6 0 1 2 3 4 5 6
௑ᫎ/ms ௑ᫎ/ms
(a) ӭౝູ (b) Ϧౝູ

图 3 快速地层条件下采用实轴积分与最速下降积分计算的井外辐射波
Fig. 3 The radiated wave calculated using real-axis integration and steepest descent integration in
the fast formation

1.5 1.5
ࠄᣉሥѬᄊፇ౧ ࠄᣉሥѬᄊፇ౧
1.0 Pฉ తᤴʾᬌሥѬᄊፇ౧ 1.0 తᤴʾᬌሥѬᄊፇ౧
Pฉ
0.5 0.5
ॆʷӑࣨए 0 Sฉ ॆʷӑࣨए 0 Sฉ

-0.5 -0.5

-1.0 -1.0

-1.5 -1.5
0 1 2 3 4 5 6 0 1 2 3 4 5 6
௑ᫎ/ms ௑ᫎ/ms
(a) ӭౝູ (b) Ϧౝູ

图 4 慢速地层条件下采用实轴积分与最速下降积分计算的井外辐射波
Fig. 4 The radiated wave calculated using real-axis integration and steepest descent integration in
the slow formation