Page 90 - 应用声学2019年第5期

842 2019 年 9 月

由式 (16) 可知，过渡段时间长度与拖船转向角 ફག
1.2 Л፶1/4ͯᎶ
度无关，因此阵上各点对拖船转向/直行的响应时间 Л፶1/2ͯᎶ
1.0 Л፶3/4ͯᎶ
和沿阵方向差变化速度仅由拖船航速和转弯半径 ፶ࡋ
决定。对于转弯角度较小的情况，靠近阵尾端的点 జဋ/T10 -3 0.8
尚未进入回转稳态就受到拖船直行的影响向直行 0.6
稳态过渡，可认为这些点受到拖船直行的影响后，沿 0.4
阵方向差停止增大，并以相同的变化速度逐渐减小。 0.2
0
5 实验结果与分析 0 200 400 600 800 1000 1200 1400 1600
௑ᫎ/s

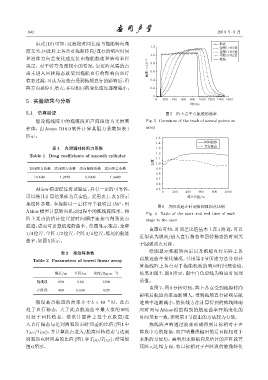
5.1 仿真验证 图 5 阵上若干点航迹的曲率
假设拖线阵中的拖缆段和声阵段均为光滑圆 Fig. 5 Curvature of the track of several points on
柱体，由 Ansys R16.0 软件计算其阻力系数如表 1 array
所示。 1.5
1.4 ړևሷগ
表 1 光滑圆柱体阻力系数 1.3 ᄰᛡሷগ
1.2
Table 1 Drag coefficients of smooth cylinder
1.1
උϙ 1.0
切向阻力系数 法向阻力系数 法向摩擦系数 法向压差系数 0.9
0.8
0.0046 1.2758 0.0309 1.2449
0.7
0.6
Ablow 模型经过海试验证，具有一定的可靠性， 0.5
0 200 400 600 800 1000
可以将其计算结果作为真实值。采用表1、表2 所示 ፶ʽͯᎶ/m
拖线阵参数，令拖船以一定转弯半径转过 150 ，用
◦
图 6 各阶段起止时刻沿圆弧顶点比例
Ablow 模型计算转向机动过程中的拖线阵阵形。将
Fig. 6 Ratio of the start and end time of each
阵上某点的估计位置按时间顺序连接可得到此点 stage to the apex
航迹，进而可计算航迹的曲率。绘图显示拖点、全阵
由图 6 可知，时间差比值基本上在 1 附近，可以
1/4位置、全阵 1/2位置、全阵 3/4位置、缆尾的航迹
近似认为脱离/进入直行稳态和回转稳态的时刻关
曲率，如图5所示。
于圆弧顶点对称。
绘图显示拖船转向后以及拖船直行后阵上各
表 2 拖线阵参数
点航迹曲率变化情况，并用第 2 节所述方法分别计
Table 2 Parameters of towed linear array
算拖线阵上各点对于拖船机动的响应时间理论值，
缆长/m 直径/m 密度/(kg·m −3 ) 结果如图 7、图 8 所示，图中白色虚线为响应时间理

拖缆段 600 0.02 1300 论值。
由图 7、图 8 分析可知，阵上各点受到拖船转向
声阵段 400 0.038 1025
影响后航迹曲率逐渐增大，受到拖船直行影响后航
假设某点航迹的曲率小于 5 × 10 −5 时，此点 迹曲率逐渐减小，特征线方法计算得到的拖线阵响
处于直行稳态，大于此点航迹曲率最大值的 90% 应时间与 Ablow 模型得到的航迹曲率开始变化的
时处于回转稳态。依次计算阵上每个点脱离/进 时间基本一致，表明第2节提出的方法较为有效。
入直行稳态与达到圆弧顶点时间差的比值 (图 1 中 拖线阵声呐通过波束形成得到目标相对于声
T AC /T CE )，并计算此点进入/脱离回转稳态与达到 阵段中心的舷角，而声呐最终输出的是目标相对于
圆弧顶点时间差的比值 (图1 中 T BC /T CD )，结果如 本船的方位角。需利用本船航向及估计的声阵段首
图6所示。 尾阵元连线方向，将目标相对于声阵段的舷角转化