Page 94 - 《应用声学》2021年第3期
P. 94
412 2021 年 5 月
从图 3 中可以看出,引起定位误差的主要因素 多普勒信息建立了v x 和v y 间的约束关系,图5中v x
是声速误差,并且声速误差引起的定位误差会随着 的取值范围为(−10, 20) m/s,且约束后的v y 取值与
脉冲传播时间的延长而增大;测向误差和测时误差 v x 的值存在映射关系,这极大地缩小了速度分量的
对定位误差的影响相对较小。仿真中目标的多普勒 取值范围。DA-SIR 算法中,v x 和 v y 的分布状态历
频移为 20 Hz 左右,目标活动区间内多普勒频移量 程图分别如图6(a)、图6(b)所示。
的变化幅度不大。
12
首先对 SIR 算法和 DA-SIR算法进行目标跟踪
仿真,进一步阐释算法的工作原理和性能提升机理。 10
算法中粒子数量均设为 10000,提取出每次更新时 8
的速度分布,形成目标跟踪过程中速度分布的历程 ᤴए v y/(mSs -1 ) 6
图,对比引入多普勒频移前后速度值分布的区别,分
析两种算法的定位精度差异。 4
2
没有引入多普勒频移时,SIR 算法假设 v x 和v y
为两个相互独立的随机过程,分别进行重采样。在 0
-10 0 10 20
跟踪过程中,v x 和 v y 分别逐渐收敛,两速度分量在 ᤴए v x /(mSs -1 )
算法跟踪过程中的分布如图4所示。
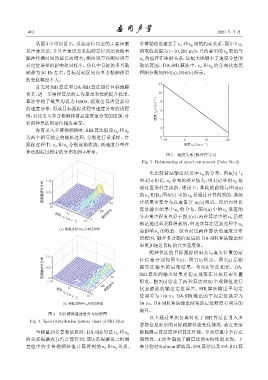
图 5 速度关系 (脉冲序号 2)
Fig. 5 Relationship of speed component (Pulse No.2)
先比较算法输出结果中 v y 的分布,图 6(b) 与
1.0 图 4(b) 相比,v y 分布的差异较大;图 4(b) 中的 v y 是
ᤴएϙፒᝠѬ࣋ 0.5 通过重采样生成的,理论上,其收敛曲线与图 4(a)
的v x 相似;图6(b) 中的v y 是通过计算得到的,其统
0 40 计结果密集分布在真值 (7 m/s) 附近。然后再对比
-10 算法输出结果中 v x 的分布,图 6(a) 中的 v x 取值的
20
0 ᑢфऀՂ 分布集中程度也好于图 4(a),两种算法中的 v x 虽然
0
10
ᤴए v x/(mSs -1 )
都是通过重采样得到的,但是在算法更新过程中 v y
(a) ᡲᢎሮ˗v x Ѭ࣋ԋሮڏ
会影响 v x 的取值。综合对比两种算法的速度分布
历程图,融合多普勒信息后的 DA-SIR 算法输出结
果更加逼近目标的真实速度值。
两种算法的目标跟踪结果及与真实位置的定
ᤴएϙፒᝠѬ࣋ 1.0 踪算法输出的局部结果,与 SIR 算法相比,DA-
位误差分别如图 7(a)、图 7(b) 所示。图 7(a) 是跟
0.5
SIR 算法的输出结果更稳定地落在目标真实位置
0
-10 40 附近。图 7(b) 给出了两种算法对 50 个观测值进行
20 ଊऀՂ
0 状态滤波的输出定位误差,SIR 算法输出平均定
0
10 位误差为 110 m,DA-SIR 输出的平均定位误差为
ᤴए v y /(mSs -1 )
(b) ᡲᢎሮ˗v y Ѭ࣋ԋሮڏ 56 m。DA-SIR算法输出结果的定位精度有明显的
提升。
图 4 SIR 滤波器速度分布历程图
以上通过单次仿真对比了 SIR 算法在引入多
Fig. 4 Speed distribution history chart of SIR filter
普勒信息前后的目标跟踪性能变化情况,意在更清
晰地展示算法原理和算法性能。单次仿真中会存在
当测量到多普勒信息时,DA-SIR 算法 v x 和 v y
的关系根据式 (17) 计算得到,图 5 是根据第二组测 偶然性,无法全面地了解算法的实际性能表现。下
量值中的多普勒频移值计算得到的 v x 和 v y 关系。 来分别对 Kalman 滤波器、SIR 算法以及 DA-SIR算