Page 67 - 《应用声学》2021年第4期

第 40 卷 第 4 期 姚振扬等： 基于 ABAQUS 的微细电火花超声振动主轴仿真研究 551

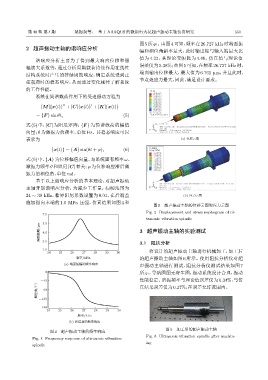
图5所示。由图4可知，频率在26.727 kHz时端面振
2 超声振动主轴的谐响应分析
幅和相位角斜率最大，此时输出端与输入端最大比
值为 4.22，其理论变幅比为 4.46，仿真值与理论值
谐响应分析主要为了得到最大响应位移和振
误差仅为5.38%；由图5可知，在频率26.727 kHz时，
幅放大系数等，通过分析周期载荷持续作用在线性
端面输出位移最大，最大值为 6.761 µm，并且此时，
结构系统时产生的持续周期响应，确定系统受到正
节点处应力最大，因此，满足设计要求。
弦载荷时的稳态响应，从而通过变化规律了解系统
的工作性能。 U֒ U 2
系统在简谐载荷作用下的受迫振动方程为

′′ ′
[M]{x(t)} + [C]{x(t)} + [K]{x(t)}
= {F } sin θt, (5)

式 (5) 中，[C] 为阻尼矩阵；{F } 为简谐载荷的幅值 X
向量；θ 为激振力的频率，单位Hz。其稳态响应可以 Y Z
表示为 (a) ͯረ̈ڏ

{x(t)} = {A} sin(θt + φ), (6) S֒ Mises
(Avg: 75%)
式(6) 中，{A} 为位移幅值向量，与系统固有频率 ω、
激振力频率θ 和阻尼 [C]有关；φ为位移响应滞后激
振力的相位角，单位rad。
基于以上谐响应分析的基本理论，对超声振动 X
主轴开展谐响应分析，为减少工作量，扫频范围为 Y Z
24 ∼ 30 kHz，临界阻尼系数设置为 0.01，在后端盖 (b) ऄҧ̈ڏ
施加指向末端的 1.6 MPa 压强，仿真结果如图 4 和
图 5 超声振动主轴的位移云图和应力云图
Fig. 5 Displacement and stress nephogram of ul-
7.0
trasonic vibration spindle
5.5
ቫ᭧૝ࣨ/mm 4.0 3 超声振动主轴的实验测试

2.5
3.1 阻抗分析
1.0 将设计的超声振动主轴进行机械加工，加工后
24 25 26 27 28 29 30
ᮠဋ/kHz 的超声振动主轴如图 6 所示。使用阻抗分析仪对超
(a) ቫ᭧૝ࣨᄊᮠဋ־ऄ
声振动主轴进行测试，阻抗分析仪测试结果如图 7
0 所示，导纳圆图无寄生圆，振动系统设计合理，振动
-45 性能稳定。谐振频率与理论值误差仅为0.34%，与仿
ᄱͯᝈ/(O) -90 真结果误差仅为0.37%，在误差允许范围内。

-135

-180
24 25 26 27 28 29 30
ᮠဋ/kHz
(b) ᄱͯᝈᄊᮠဋ־ऄ
图 6 加工后的超声振动主轴
图 4 超声振动主轴的频率响应
Fig. 6 Ultrasonic vibration spindle after machin-
Fig. 4 Frequency response of ultrasonic vibration
ing
spindle