Page 86 - 《应用声学》2021年第6期

882 2021 年 11 月

1.3 阶梯圆环径向振动性能分析 下能够实现由内向外的径向位移振幅放大。表 1 为
选取阶梯型圆环的材料为硬铝，材料参数 理论计算和有限元仿真的阶梯圆环在不同的径向
σ = 0.33，E = 71 GPa，ρ = 2810 kg/m 。阶梯 尺寸下其一阶和二阶径向共振频率值。
3
圆环的内外环轴向厚度分别为 10 mm 和 3 mm，改 在表 1 中，f a1 和 f a2 分别表示理论计算得出的
变内环的外半径，可得其一阶、二阶径向共振频 一阶和二阶径向共振频率值，f b1 和 f b2 分别为仿真
率与内外环径向厚度之比 K 1 的变化关系，其中 模拟得出的一阶和二阶径向共振频率值，∆f 1ab 和
K 1 = (R 1 − R)/(R 2 − R 1 )。理论计算和仿真结果 ∆f 2ab 分别为两种方法计算得出的一阶、二阶径向
如图5和表1所示。 共振频率值的相对误差。由表1可知，K 1 值增大，阶
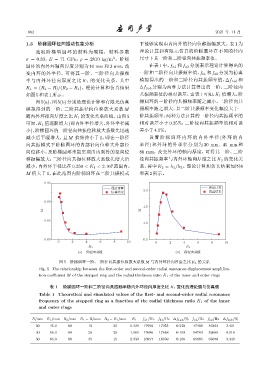
图 5(a)、图 5(b) 分别是理论计算和有限元仿真 梯圆环的一阶径向共振频率随之减小，二阶径向共
模拟得到的一阶、二阶共振径向位移放大系数 M 振频率随之增大，且二阶共振频率变化幅度大于一
随内外环径向厚度之比K 1 的变化关系曲线。由图 5 阶共振频率；两种方法计算的一阶径向共振频率的
可知，K 1 值逐渐增大(即内环半径增大，外环半径减 相对误差小于 0.25%，二阶径向共振频率的相对误
小)，阶梯圆环的一阶径向共振位移放大系数先迅速 差小于4.5%。
减小后平缓增大，且 M 值始终小于 1，即在一阶径 设 置 阶 梯 圆 环 内 环 的 内 外 半 径 (外 环 的 内
向共振模式下阶梯圆环的内部径向位移大外部径 半径) 和外环的外半径分别为 30 mm、45 mm 和
向位移小，及阶梯圆环未能实现由内到外的径向位 80 mm，改变外环的轴向厚度，可得其一阶、二阶
移振幅放大；二阶径向共振位移放大系数先增大后 径向共振频率与内外环轴向厚度之比 K 2 的变化关
减小，内外环半径比在 0.250 < K 1 < 3.167 范围内， 系，其中 K 2 = h 1 /h 2 。理论计算和仿真结果如图 6
M 值大于 1，在此范围内阶梯圆环在二阶共振模式 和表 2所示。

0.95
ေ᝷ᝠካ ေ᝷ᝠካ
͌ᄾፇ౧ 2.0 ͌ᄾፇ౧
0.90
1.5
M M

0.85
1.0

0.80 0.5
0 2 4 6 8 10 0 2 4 6 8 10
K  K 
(a) ʷ᫽य़ՔС૝ (b) ̄᫽य़ՔС૝

图 5 阶梯圆环一阶、二阶径向共振位移放大系数 M 与内外环径向厚度之比 K 1 的关系
Fig. 5 The relationship between the first-order and second-order radial resonance displacement amplifica-
tion coefficient M of the stepped ring and the radial thickness ratio K 1 of the inner and outer rings

表 1 阶梯圆环一阶和二阶径向共振频率随内外环径向厚度之比 K 1 变化的理论值与仿真值
Table 1 Theoretical and simulated values of the first- and second-order radial resonance
frequency of the stepped ring as a function of the radial thickness ratio K 1 of the inner
and outer rings

R/mm R 1 /mm R 2 /mm R 1 − R/mm R 2 − R 1 /mm K 1 f a1 /Hz f b1 /Hz ∆f 1ab /% f a2 /Hz f b2 /Hz ∆f 2ab /%
30 45.0 80 15 35 0.429 17996 17955 0.228 47489 46362 2.431
30 55.0 80 25 25 1.000 17686 17658 0.159 54783 52668 4.016
30 65.0 80 35 15 2.333 16957 16939 0.106 65185 63078 3.340