Page 89 - 《应用声学》2021年第6期

第 40 卷 第 6 期 许龙等： 阶梯圆环压电超声换能器径向振动性能的理论研究 885

2.2 阶 梯 圆 环 压 电 超 声 换 能 器 径 向 振 动 性 能 振、反共振频率值，∆f 1mc 、∆f 1nc 和 ∆f 2mc 、∆f 2nc
的分析 分别为两种方法计算的一阶径向共振、反共振频率

图 7 所示的阶梯圆环压电超声换能器中 a = 值的相对误差和二阶径向共振、反共振频率值的相
6 mm，R = 30 mm，R 1 = 45 mm，R 2 = 80 mm。 对误差，K eff1 和K eff2 分别为理论计算的一阶、二阶
换能器的压电陶瓷圆环材料为 PZT-4，其材料参 共振模式下的有效机电耦合系数，K eff1 和 K eff2 分
′
′
3
数为 ρ 0 = 7500 kg/m ，ε T = 11.4946 × 10 −9 ，
33 别为仿真模拟的一阶、二阶共振模式下的有效机电
d 31 = −123 × 10 −12 C/N，σ 0 = 0.33，S E =
11 耦合系数。由表3可知，两种方法计算的换能器的一
2
E
2
12.3 × 10 −12 m /N，S 12 = −4.05 × 10 −12 m /N， 阶、二阶径向共振和反共振频率的相对误差均小于
h 0 = 10 mm，阶梯圆环的材料参数与 1.3 节相同，
2%，一阶共振模式下换能器的有效机电耦合系数整
h 1 = 10 mm，h 2 = 3 mm。根据以上换能器的材料
体大于二阶共振模式下的有效机电耦合系数。由此
参数和结构尺寸参数分别用等效电路法和有限元
可知，阶梯圆环压电超声换能器等效电路模型具有
法计算了阶梯圆环压电超声换能器的径向共振、反
较高的设计精度。
共振频率、有效机电耦合系数，通过有限元仿真模
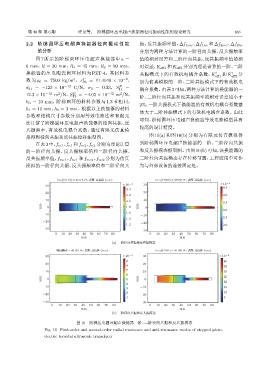
拟得到径向共振和反共振位移振型图。 图 10(a) 和图 10(b) 分别为有限元仿真模拟得
在表3中，f m1 、f n1 和f m2 、f n2 分别为理论计算 到阶梯圆环压电超声换能器的一阶、二阶径向共振
的一阶径向共振、反共振频率值和二阶径向共振、 和反共振模态振型图。由图10(b)可知，该换能器的
反共振频率值，f mc1 、f nc1 和 f mc2 、f nc2 分别为仿真 二阶径向共振模态存在位移节圆，工程应用中可作
模拟的一阶径向共振、反共振频率值和二阶径向共 为与外部设备的连接固定处。

freq(15119)=25118 Hz ᛫᭧ ঴ͯረ (mm) freq(17037)=27036 Hz ᛫᭧ ঴ͯረ (mm)
30 T10 -3 30 T10 -4
2.4 4.5
20 20
2.2 4.0
10 2.0 10
3.5
mm 0 1.8 mm 0
3.0
1.6
-10 -10
1.4 2.5
-20 -20
1.2 2.0
-30
-30
0 10 20 30 40 50 60 70 80 0 10 20 30 40 50 60 70 80
mm mm
(a) ʷ᫽य़ՔС૝֗ԦС૝വগ
ྲढ़ᮠဋ=40153 Hz ᛫᭧ ঴ͯረ (mm) freq(31181)=41180 Hz ᛫᭧ ঴ͯረ (mm)
30 T10 -4 30 T10 -5
9 40
20 20
8 35
7
10 10 30
6
mm 0 5 mm 0 25
4 20
-10 -10 15
3
2 10
-20 -20
1 5
-30 -30
0 10 20 30 40 50 60 70 80 0 10 20 30 40 50 60 70 80
mm mm
(b) ̄᫽य़ՔС૝֗ԦС૝വগ
图 10 阶梯压电圆环超声换能器一阶、二阶径向共振和反共振模态
Fig. 10 First-order and second-order radial resonance and anti-resonance modes of stepped piezo-
electric toroidal ultrasonic transducer