Page 32 - 《应用声学》2022年第1期

28 2022 年 1 月

运算复杂度分析相吻合。由图 4 可知单节点 WPE 法结果各项指标相对于原始信号 (Ref) 的提升值。
算法最快收敛至稳定，但语声质量提升性能不及集 每个位置、每种混响时间同样进行 60 次实验。由
中式算法与分布式算法；由于分布式算法中每节点 图 5 可知，分布式算法能够达到集中式算法的性能，
的滤波器系数维度小于集中式，因此在更新初期性 且明显优于使用通道数较少的单节点WPE算法。
能与收敛速度上均优于集中式算法，分布式算法于
3.3 分布式WPE算法对噪声鲁棒性测试
3 s 左右达到稳定，集中式算法于 6 s 左右达到稳定，
两者稳定后客观指标性能处于同一水平。 假设环境为球各向同性噪声声场 (Spherically
isotropic noise filed)，除30 dB 本底噪声外，给传声
0.5
器注入不同程度的扩散噪声 [35] 。图 6 展示了分别
0.4
0.3 注入 10 dB、15 dB、20 dB、25 dB、30 dB 扩散噪
0.2 声时，说话人位于位置 1、T 60 = 650 ms 以及说话
PESQଢӤ 0.1 0 Single Node1-WPE 人位于位置 3、T 60 = 900 ms 两种情况下，集中式

-0.1
Single Node3-WPE
-0.2 Single Node2-WPE (Cen-WPE)、分布式 (DWPE)及单节点(SN-WPE)
Cen-WPE
-0.3 算法结果的各项评价指标。大部分情况下，分布式
DWPE
-0.4
算法与集中式算法依旧好于单节点算法输出，但由
0 1 2 3 4 5 6 7 8 9 10
௑ᫎ/s 于 WPE 算法无降噪能力，随着噪声量的增加，λ 的
(a) 650 msຉ־ ͯᎶ1 估计准确度下降、各算法输出结果在混响部分的差
异降低，3 种算法的性能逐渐接近；此外，从所有测
0.5
0.4 试指标均可看出，随噪声量增加，分布式算法的稳定
0.3
性优于集中式算法。
0.2
PESQଢӤ 0.1 0 Single Node1-WPE 3.4 主观测听测试

Single Node2-WPE
-0.1
Single Node3-WPE 为了进一步测试 DWPE 算法性能，借鉴文
-0.2
Single Node4-WPE 献 [36] 的方法，采用主观测听的方法进行了 DWPE
-0.3 Cen-WPE
-0.4 DWPE 算法与集中式算法以及 DWPE 算法与单节点算法
0 1 2 3 4 5 6 7 8 9 10 对混响语声处理性能的对比测试。从 TIMIT 数据
௑ᫎ/s
库中选取 6 名女性、6 名男性，共 12 名说话人语声，
(b) 900 msຉ־ ͯᎶ3
生成 650 ms、900 ms 或1100 ms 三种程度的混响信
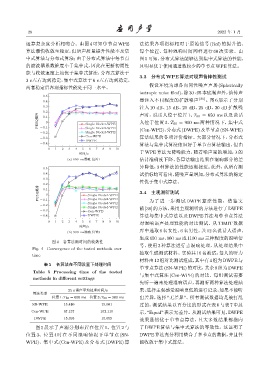
图 4 各算法随时间的收敛性
号，使用 3 种算法进行去混响处理，从处理结果中
Fig. 4 Convergence of the tested methods over
抽取生成测试材料。实验共 16 名被试，每人的听力
time
材料由12组对比测试组成，其中有4组为DWPE与
表 5 各算法在不同设置下处理时间
单节点算法 (SN-WPE) 的对比，其余 8 组为 DWPE
Table 5 Processing time of the tested
与集中式算法 (Cen-WPE) 的对比。每组测试需要
methods in different settings
先听一遍未处理混响语声，再测听两种算法处理结
25 s 语声平均处理时间/s 果，选择主观感受混响更低的进行记录，如果不能听
算法类型
位置 1、T 60 = 650 ms 位置 3、T 60 = 900 ms 出差异，选择 “无差异”。所有测试数据均是被打乱
SN-WPE 15.410 15.001 过的，测试结果以百分比的形式在表 6 与表 7 中展
Cen-WPE 67.137 102.110 示，“Equal” 表示无差异。从测试结果可见，DWPE
DWPE 15.393 15.659
效果显然优于单节点算法，且大多数结果都指向
图 5 展示了声源分别布置在位置 1、位置 2 与 了 DWPE 算法与集中式算法的等效性。这证明了
位置 3、位置 4 时在不同混响情况下单节点 (SN- DWPE算法充分利用整合了多节点的数据，并且性
WPE)、集中式 (Cen-WPE) 及分布式 (DWPE) 算 能收敛于集中式算法。