Page 49 - 《应用声学》2022年第5期

第 41 卷 第 5 期 左炜翌等： 非线性兰姆波在厚度缓慢变化和衰减下的特性分析 725

2.5 3.0
ᛰѓ ᛰѓ
௄ᛰѓ ௄ᛰѓ
2.5
2.0
૝ࣨ/(10 -8 m) 1.5 ૝ࣨ/(10 -7 m) 2.0

1.5
1.0
1.0

0.5
0.5
0 0
0 0.2 0.4 0.6 0.8 1.0 0 0.2 0.4 0.6 0.8 1.0
͜୧ᡰሏ/m ͜୧ᡰሏ/m
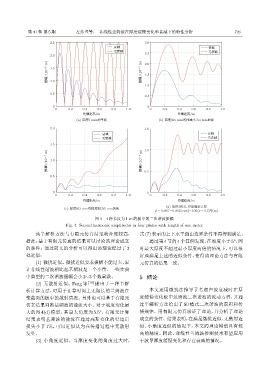
(a) Ԓए5 mmᄊࣱ౜ (b) Ԓए̰5 mmጳভѓ࠵˞3 mmᄊ౜
2.0 1.5
ᛰѓ ᛰѓ
௄ᛰѓ ௄ᛰѓ
1.5 1.0
૝ࣨ/(10 -7 m) 1.0 ૝ࣨ/(10 -7 m)

0.5 0.5

0 0
0 0.2 0.4 0.6 0.8 1.0 0 0.2 0.4 0.6 0.8 1.0
͜୧ᡰሏ/m ͜୧ᡰሏ/m
(d) ݠڏ3ਫ਼ᇨ Ԓए໘ᡜவሮ
(c) Ԓए̰3 mmጳভܙҫ˞5 mmᄊ౜
2
d=0.005-0.0015exp[-100(x-0.3) ](m)
图 4 4 种长度为 1 m 的板中的二次谐波振幅
Fig. 4 Second harmonic amplitudes in four plates with length of one meter
该半解析方法与有限元仿真结果吻合度较高， 式 (7)表示的上下水平自由边界条件不再得到满足。
据此，基于有限元仿真的结果可以讨论该理论成立 通过第 4 节的 4 个算例发现，在坡度小于 5°，同
的条件。通过前文的分析可以得出该理论经过了 3 时最大厚度不超过最小厚度两倍的情况下，可以很
处近似： 好地满足上述的近似条件，使得该理论方法与有限
(1) 微扰近似。微扰近似要求振幅不能过大，累 元仿真的结果一致。
计非线性谐波相比起基频波是一个小量。一些实验
中典型的二次谐波振幅会小2∼3个数量级。 5 结论
(2) 无散射近似。Feng 等 [16] 提出了一种半解
析计算方法，可用于计算时间上无限长的兰姆波在 本文运用微扰法推导了考虑声波衰减时在厚
变截面的板中的散射情况。另外也可以基于有限元 度缓慢变化板中兰姆波二次谐波的波动方程，并通
仿真结果判断基频波的能流大小。对于坡度变化最 过半解析方法给出了 S0 模式二次谐波的累积和传
大的图 4(d) 模型，其最大角度为 5.5°，有限元计算 播规律。用有限元仿真验证了理论，并分析了理论
结果表明基频波的能流在通过高斯变化的窄边后 成立的条件。结果表明，在满足微扰近似、无散射近
损失小于 1%，可以近似认为在传播过程中无散射 似、小角度近似的情况下，本文的理论模型具有较
发生。 高的精度。因此，非线性兰姆波检测技术有望应用
(3) 小角度近似。当厚度变化的角度过大时， 于波导厚度缓慢变化和存在衰减的情况。