Page 54 - 《应用声学》2022年第5期

730 2022 年 9 月

表 1 铝合金材料参数 NT11
+30.07
Table 1 Material properties of aluminum alloy +29.23
+28.39
+27.56
+26.72
+25.88
+25.04
材料属性 数值 +24.20
+23.36
+22.52
弹性模量/GPa 70 +21.68
+20.81
+20.00
泊松比 0.33
密度/(kg·m −3 ) 2780
2
◦
热传导系数/(W·(m · C) −1 ) 121
◦
比热容/(J·(kg· C) −1 ) 875
热膨胀系数/K −1 22
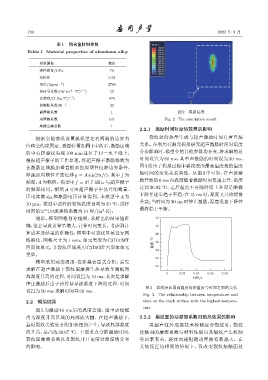
静摩擦系数 1 图 2 模拟结果
动摩擦系数 0.5 Fig. 2 The simulation result
摩擦衰减系数 1
2.2.1 激励时间对励热效果的影响
根据实验情况设置板模型左右两端的边界为 裂纹处的热量生成与超声激励时间有着直接
位移全约束固定。激励位置如图1中所示，激励区域 关系。在利用有限元模拟研究超声激励时间对温度
的中心距裂纹尖端 100 mm 且位于同一水平线上。 分布影响时，模型中的其他参数均不变，将求解的总
根据超声振子的工作原理，将超声振子激励等效为 时间设置为 80 ms，其中声激励的时间设为 30 ms。
在激励区域施加垂直板面的周期性位移边界条件， 图3 给出了模拟过程中裂纹表面最高温度处的温度
即施加周期性正弦位移 y = A sin(2πft)，其中 f 为 随时间的变化关系曲线。从图 3 中可知，在声波激
频率，A 为幅值。模型中 f = 37.7 kHz，与超声振子 励开始的6 ms内温度随着激励时间快速上升，温度
达到 30.02 C；之后温度不再随时间上升而是略微
◦
的频率相同。幅值 A 可由超声振子中晶片的数量、
下降并逐步趋于平稳；在15 ms时，温度又开始缓慢
压电常数 d 33 和激励电压计算得到，本模型中 A 为
升高；当时间为30 ms时停止激励，温度迅速下降并
10 µm。模型中试样的初始温度设置为 20 C，试样
◦
最终趋于平衡。
2
周围的空气对流换热系数为10 W/(m ·K)。
通常，模型网格划分越细，求解出的结果越准 32
确，但会导致计算量增大、计算时间变长。考虑到计 30
算成本及结果的准确性，模型中对裂纹区域进行网 28
格细化，网格尺寸为 1 mm，单元类型为 C3D10MT ພए/Ć 26
四面体单元，非裂纹区域采用 C3D8RT 六面体单元
24
类型。
22
模型采用动态温度 -位移耦合显式分析，首先
20
求解在超声激励下裂纹面摩擦生热导致金属板局
0 0.02 0.04 0.06 0.08
部温度升高的过程，时间设置为 10 ms；其次是求解 ௑ᫎ/s
停止激励后由于热传导导致温度下降的过程，时间
图 3 裂纹表面最高温度处的温度与时间之间的关系
设置为50 ms，求解时间共60 ms。
Fig. 3 The relationship between temperature and
2.2 模拟结果 time on the crack surface with the highest tempera-
ture
图 2 为激励 10 ms 后的温度云图，图中虚线框
内为温度升高区域的局部放大图。在超声激励下， 2.2.2 裂纹面的动摩擦系数对励热效果的影响
靠近裂纹尖端处有附加热量的产生，导致局部温度 用超声红外成像技术检测疲劳裂纹时，裂纹
的升高，最高达 30.07 C。下面重点分析激励时间， 接触面的摩擦系数与材料性能以及裂纹产生机制
◦
裂纹面摩擦系数以及裂纹开口宽度对温度场分布 等因素有关，裂纹面越粗糙动摩擦系数越大。在
的影响。 其他设置均相同的情况下，仅改变裂纹接触面处