Page 117 - 《应用声学》2023年第1期

第 42 卷 第 1 期 王泽茜等： 理想浅海波导中声场奇异点与声源深度的关系 113

0 0 0
37.5 37.5 37.5

z t /m 75.0 z t/m 75.0 z t/m 75.0

112.5 112.5 112.5

150.0 150.0 150.0
-100 -50 0 50 100 -100 -50 0 50 100 -100 -50 0 50 100
R/m R/m R/m
(a) (1,7)-AMG sd=25 m (b) (1,7)-AMG sd=50 m (c) (1,7)-AMG sd=75 m
0 0 0

37.5 37.5 37.5
z t /m 75.0 z t/m 75.0 z t/m 75.0

112.5 112.5 112.5
150.0 150.0 150.0
-100 -50 0 50 100 -100 -50 0 50 100 -100 -50 0 50 100
R/m R/m R/m
(d) (1,7)-AMG sd=100 m (e) (1,7)-AMG sd=125 m (f) (1,7)-AMG sd=150 m
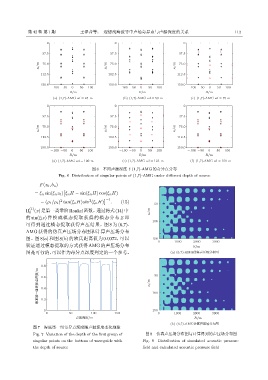
图 6 不同声源深度下 (1,7)-AMG 的奇异点分布
Fig. 6 Distribution of singular points of (1,7)-AMG under different depth of source

F(z 0 , b n )
[
= ξ n sin(ξ n z 0 ) ξ n H − sin(ξ n H) cos(ξ n H)
2
2
− (ρ 1 /ρ 2 ) tan(ξ n H) sin (ξ n H) ] −1 . (15)
50
H (1) (x)是第一类零阶Hankel函数。通过将式(14)中
0 z t /m
的 sin(ξ l z) 替换成模态提取获得的模态分布 Z 即
100
可得到通过模态提取获得声压结果。图 8 为 (6,7)-
AMG 获得的仿真声压场分布图和计算声压场分布
图。图 8(a) 和图 8(b) 的欧氏距离仅为 0.0072，可以 150
0 1000 2000 3000
验证通过模态提取的方式获得 AMG 的声压场分布 R/m
图是可行的，可以作为奇异点深度判定的一个参考。 (a) (6,7)-AMG͌ᄾܦԍڤѬ࣋ڏ

0.8 50
๒अኄʷጸ݉पགງए/m 0.6 z t/m 100

0.4

0.2

0 150
0 50 100 150 0 1000 2000 3000
ܦູງए/m R/m
(b) (6,7)-AMGᝠካܦԍڤѬ࣋ڏ
图 7 海底第一组奇异点深度随声源深度变化规律
Fig. 7 Variation of the depth of the first group of 图 8 仿真声压场分布图与计算得到的声压场分布图
singular points on the bottom of waveguide with Fig. 8 Distribution of simulated acoustic pressure
the depth of source field and calculated acoustic pressure field