Page 118 - 《应用声学》2023年第1期

114 2023 年 1 月

4.2 求逆运算获取声源深度 0
10
如果将浅海仿真参数按表 1 来设定，奇异点
20
的分布仅与 AMG 的阶数、阶差以及声源深度有 30
关。由公式 (8)、公式 (9) 以及图 7 可知，第一组奇 40
50
异点深度 (AMG 声压场近零点深度) 和声源深度有 60
关。将 50 Hz 声源放置在波导 100 m 深度处，得到 ܦູງए/m 70
(6,7)-AMG水平距离满足cos[(ξ l −ξ q )R] = −1的第 80
一组奇异点深度分别约为：22.8 m、46.6 m、71.5 m、 90
100
96.2 m、121.1 m、146 m，这组奇异点深度对应公 110 100 m
式 (9)，将 z 代入公式 (9) 得到的结果如图 9 所示，图 120
中横坐标为不同声源深度Z 0 代入公式(9)的值。由 130 (5,7)-AMG
140 (6,7)-AMG
图看出通过一个 AMG 求解的声源深度不唯一，为
150
-2 -1 0 1 2
了找到准确的声源深度，需要引入辅助 AMG，通过
cos(b l Z  )cos(b l zϕ)-cos(b q Z  )cos(b q zϕ)
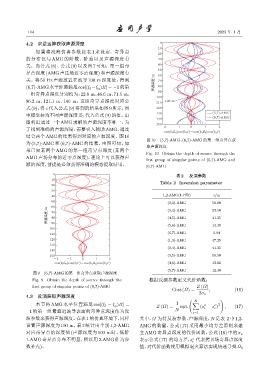
结合两个 AMG 的结果得到对应的声源深度。图10
图 10 (5,7)-AMG、(6,7)-AMG 的第一组奇异点获
为 (5,7)-AMG 和 (6,7)-AMG 的结果，由图可知，如
取声源深度
果已知某两个 AMG 的第一组奇异点深度 (某两个
Fig. 10 Obtain the depth of source through the
AMG 声场分布的近零点深度)，理论上可以获得声
first group of singular points of (5,7)-AMG and
源的深度，前提是必须获得准确的模态提取结果。 (6,7)-AMG
0
表 2 反演参数
10
Table 2 Inversion parameter
20
30
40 1,2-AMG(1-7 阶) z/m
50
(2,3)-AMG 58.80
60 (3,4)-AMG 23.50
ܦູງए/m 70 (4,5)-AMG 41.35
80
90
(5,6)-AMG 14.48
100
110 (6,7)-AMG 0.94
120 (1,3)-AMG 47.29
130
(2,4)-AMG 41.35
140
150 (3,5)-AMG 58.50
-2 -1 0 1 2
cos(b l Z  )cos(b l zϕ)-cos(b q Z  )cos(b q zϕ) (4,6)-AMG 13.82
(5,7)-AMG 12.40
图 9 (6,7)-AMG 的第一组奇异点获取声源深度
Fig. 9 Obtain the depth of source through the 根据反演参数定义代价函数：
first group of singular points of (6,7)-AMG Z (Ω)
Cost (Ω) = , (16)
2σ z
4.3 反演获取声源深度
( )
N
本节将 AMG 水平位置满足 cos[(ξ l − ξ q )R] = 1 ∑ e c 2
Z (Ω) = sqrt (z − z ) , (17)
i
i
−1 的第一组最靠近波导表面的奇异点深度作为反 N i=1
演参数来获得声源深度。在表1的仿真环境下，同样 其中，Ω 为待反演参数 -声源深度，N 是表 2 中 1,2-
设置声源深度为 100 m，表 2 统计出个别 1,2-AMG AMG 的数量，公式 (17) 采用最小均方差原则来建
对应奇异点的深度值 (声源深度为 100 m 时，低阶 立 AMG 奇异点深度的代价函数，公式 (16) 中的 σ z
1-AMG 奇异点分布不明显，所以用 2-AMG 作为参 表示公式(17) 的均方差，z 代表拷贝场奇异点深度
c
i
数补充)。 值。对代价函数使用模拟退火算法实现快速寻找Ω 0