Page 10 - 《应用声学》2023年第3期

448 2023 年 5 月

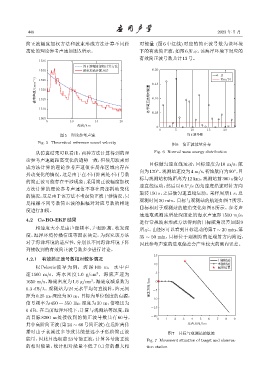
简正波幅度加权方法和波束形成方法计算不同距 对能量 (图 6 中红线) 对应的简正波号数为该环境
离处的理论参考声速如图5所示。 下的有效简正波，如图6所示，该海洋环境下对应的
有效简正波号数共计13号。
1535
እ൤ฉࣨएҫిᝠካவข
1530 ฉౌॎੇᝠካவข 0.20
E
ԠᏦܦᤴ/(mSs -1 ) 1520 ՊՂእ൤ฉᄱࠫᑟ᧚ 0.15
Em/10
1525

0.10
1515
1510 0.05
1505
5 10 15 20
ᡰሏ/km
0
0 5 10 15 20
图 5 理论参考声速 እ൤ฉՂ஝
Fig. 5 Theoretical reference sound velocity
图 6 简正波能量分布
从仿真结果可以看出，两种方法计算得到的理 Fig. 6 Normal wave energy distribution
论参考声速随距离变化的趋势一致，但使用波束形
目标做匀速直线运动，目标速度为 10 m/s，航
成方法计算的理论参考声速值在局部区域内存在
向为170 。观测站速度为4 m/s，初始航向为90 ，目
◦
◦
抖动变化的情况，这是由于在不同距离处不同号数
标与观测站初始距离为12 km。观测站前300 s做匀
的简正波可能存在干涉现象；采用简正波幅度加权
速直线运动，然后以 0.5 /s 的角速度沿逆时针方向
◦
方法计算的理论参考声速值不存在局部抖动变化
旋转 150 s，之后做匀速直线运动。采样周期 1 s，总
的情况，这是由于该方法不考虑简正波干涉情况，只
观测时间50 min。目标与观测站的航迹如图7所示，
是根据不同号数简正波的振幅对对应号数的相速
目标相对于观测站的舷角变化如图 8 所示。参考声
度进行加权。
速选取观测站所处深度处的海水声速即 1500 m/s，
4.2 Cs-BO-EKF结果
进行常规波束形成方法得到的目标舷角误差如图 9
相速度大小是由声源频率、声源距离、收发深 所示。由图8可以看到目标运动的第7 ∼ 20 min、第
度、海洋环境传播信道等因素决定，为探究该方法 35 ∼ 50 min，目标位于观测站的近端射方向附近，
对于海洋环境的适应性，分别以不同海洋环境下阵 因此参考声速的选取偏差会产生较大的测向误差。
列接收到的有效简正波号数多少进行讨论。
15
4.2.1 有效简正波号数相对较多情况 ᄬಖᢾᤜ
10 వᓍᢾᤜ
以 Pekeris 波导 为 例， 海 深 100 m， 水中声 ᡑݽͯᎶ
3
速 1500 m/s，海水密度 1.0 g/cm ，海底声速为 5
3
1650 m/s，海底密度为 1.6 g/cm ，海底衰减系数为 0
0.3 dB/λ。观测站为 24 元水平均匀直线阵，阵元间 ӯӒவՔ/km -5
距为0.25 m，深度为30 m。目标为单位强度的点源，
-10
信号频率为 450 ∼ 550 Hz，深度为 30 m，信噪比为
-15
0 dB。在当前海洋环境下，计算与观测站等深度，距
离目标 8200 m 处接收到的简正波号数共有 60 号， -20 0 1 2 3 4 5 6 7 8 9
其中高阶简正波 (第24 ∼ 60 号简正波) 在远距离传 ˌ᜵வՔ/km
播时由于衰减过多导致其能量远小于低阶简正波 图 7 目标与观测站的航迹
能量，因此只选取前 23 号简正波，计算各号简正波 Fig. 7 Movement situation of target and observa-
的相对能量，统计相对能量不低于 0.1 倍的最大相 tion station