Page 11 - 《应用声学》2023年第3期

第 42 卷 第 3 期 李鑫等： 水平线列阵方位 -相速度联合的卡尔曼滤波方法 449

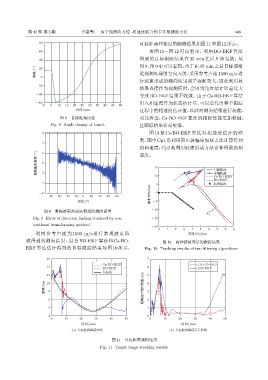
80 目标距离和速度的跟踪结果如图11和图12所示。
60 由图 10∼ 图 12 可以看出，利用 BO-EKF 算法
得到的目标跟踪结果在 35 min 之后开始发散，从
40
图 8、图 9 中可以看到，由于在 35 min 之后目标逐渐
ᝈए/(°) 近观测站端射方向入射，采用参考声速1500 m/s 进
20
0
行波束形成的测向结果误差逐渐变大，因此采用其
-20
结果直接作为观测值时，会因为角度估计误差过大
-40
导致 BO-EKF 结果不收敛。由于 Cs-BO-EKF 算法
-60 引入相速度作为状态估计量，可以迭代出整个跟踪
0 5 10 15 20 25 30 35 40 45 50
௑ᫎ/min 过程中的相速度估计值，以此对测向结果进行校准，
图 8 目标舷角历程 对比看出，Cs-BO-EKF 算法的跟踪性能更加稳健，
Fig. 8 Angle change of target 且跟踪结果误差更低。
6 图 13 是 Cs-BO-EKF 算法对相速度估计的结
果，图中 Cp1 是利用简正波幅度加权方法计算得到
4
的相速度，Cp2 是利用波束形成方法计算得到的相
Ϡሏᄾࠄᝈए/(°) 0 15 ᄬಖᢾᤜ
2
速度。

వᓍᢾᤜ
-2
10
Cs-BO-EKF
BO-EKF
-4 5 ᡑݽᓈᤜ
ӯӒவՔ/km
-6 0
-80 -60 -40 -20 0 20 40 60 80
ᝈए/(°) -5
图 9 常规波束形成法得到的测向误差 -10
Fig. 9 Error of direction finding obtained by con- -15
ventional beamforming method
-20
0 1 2 3 4 5 6 7 8 9
利用参考声速为 1500 m/s 进行常规波束形 ˌ᜵வՔ/km
成得到的测向结果，结合 BO-EKF 算法和 Cs-BO- 图 10 两种滤波算法的跟踪结果
EKF 算法估计得到的目标跟踪结果如图 10 所示， Fig. 10 Tracking results of two filtering algorithms

16 7
Cs-BO-EKF Cs-BO-EKF
14 6
BO-EKF BO-EKF
ᄾࠄϙ
12 5
ᡰሏ/km 10 8 ᡰሏͥᝠᄱࠫឨࣀ/km 4 3

6 2

4 1
2 0
0 10 20 30 40 50 0 10 20 30 40 50
௑ᫎ/min ௑ᫎ/min
(a) ᄬಖᡰሏᡲᢎజጳ (b) ᄬಖᡰሏᡲᢎឨࣀజጳ

图 11 目标距离跟踪结果
Fig. 11 Target range tracking results