Page 12 - 《应用声学》2023年第3期

450 2023 年 5 月

12 6
Cs-BO-EKF
5
10 4 BO-EKF
ᤴए/(mSs -1 ) 8 ᤴएͥᝠፐࠫឨࣀ/(mSs -1 ) 3

Cs-BO-EKF 2
6
BO-EKF
ᄾࠄϙ 1
4 0
0 10 20 30 40 50 0 10 20 30 40 50
௑ᫎ/min ௑ᫎ/min
(a) ᄬಖᤴएᡲᢎజጳ (b) ᄬಖᤴएᡲᢎឨࣀజጳ

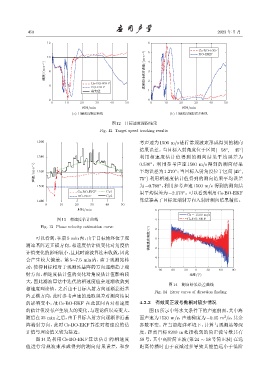
图 12 目标速度跟踪结果
Fig. 12 Target speed tracking results

1560 考声速为 1500 m/s 进行常规波束形成得到的测向
结果误差。当目标入射角度位于区间 [−58 , −45 ]
◦
◦
1540 利用相速度估计值得到的测向结果平均误差为
0.530 ，利用参考声速 1500 m/s 得到的测向结果
◦
ܦᤴ/(mSs -1 ) 1520 平均误差为 1.270 ；当目标入射角度位于区间 [45 ,
◦
◦
75 ] 利用相速度估计值得到的测向结果平均误差
◦
◦
1500 为 −0.768 ，利用参考声速 1500 m/s 得到的测向结
Cs-BO-EKF Cp1 果平均误差为−2.173 。可以看到利用Cs-BO-EKF
◦
BO-EKF Cp2
1480 算法提高了目标近端射方向入射时测向结果精度。
0 10 20 30 40 50
௑ᫎ/min 6
Cs=1500 m/s
图 13 相速度估计曲线 4 Cs-BO-EKF
Fig. 13 Phase velocity estimation curve 2
Ϡሏᄾࠄᝈए/(°)
可以看到，在前5 min 内，由于目标始终位于观 0
测站基阵近正横方向，相速度估计值变化对角度估 -2
计值变化的影响较小，且此时滤波算法未收敛，因此
-4
会产生较大偏差。第 5∼7.5 min 内，由于观测站转
动，使得目标相对于观测站基阵的方向逐渐趋于端 -6
-90 -60 -30 0 30 60 90
射方向，相速度估计值的变化对角度估计值影响较 ᝈए/(°)
大，因此滤波算法中迭代的相速度值会逐渐收敛到
图 14 测向结果误差曲线
相速度理论值。之后由于目标入射方向逐渐靠近基
Fig. 14 Error curve of direction finding
阵正横方向，此时参考声速的选取误差对测向结果
的影响变小，故 Cs-BO-EKF 在此区间内对相速度 4.2.2 有效简正波号数相对较少情况
的估计值没有产生较大的变化，与理论值误差变大。 图15所示中等水文条件下的声速剖面，其中海
2
随后在 35 min 之后，由于目标入射方向逐渐靠近基 面声速为 1530 m/s，声速梯度为 −0.05 m /s，其余
阵端射方向，此时 Cs-BO-EKF 算法对相速度的估 参数不变。在当前海洋环境下，计算与观测站等深
计值与理论值又较为接近。 度，距离目标 8200 m 处接收到的简正波号数共有
图 14 是利用 Cs-BO-EKF 算法估计的相速度 58 号，其中高阶简正波 (第 24 ∼ 58 号简正波) 在远
值进行常规波束形成得到的测向结果误差，和参 距离传播时由于衰减过多导致其能量远小于低阶