Page 117 - 《应用声学）》2023年第5期

第 42 卷 第 5 期 王卓越等： 基于倾斜阵的距离与方位联合估计 1009

ေ᝷ಫ౤Ѧ஝
1.0
c w=1500 m/s 5
ρ w =1000 kg/m 3 0.8
ඵງ100 m
α w =6T10 -5 dB/λ 10 0.6
᫼ѵᡰሏ/m 15 ࣨए/dB

c b=1700 m/s 20 0.4
෢᠏अᦊ ρ b=1900 kg/m 3 0.2
α b=0.8 dB/λ
25
300 400 500 600
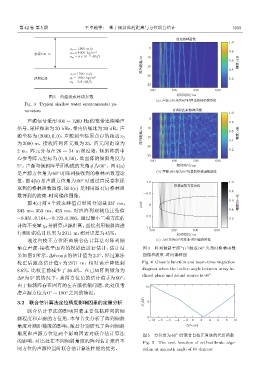
图 3 典型浅水环境参数 ᄱࠫ௑ᫎ/ms
(a) ܦູவͯᝈ˞60°௑ေ᝷ಫ౤Ѧ஝ڏϸ
Fig. 3 Typical shallow water environmental pa-
rameters ᄯԄሥଢԩಫ౤Ѧ஝
1.0
声源信号采用 400 ∼ 1200 Hz 的宽带连续噪声 5 0.8
信号，采样频率为 20 kHz，带内信噪比为20 dB。声 10 0.6

源坐标为 (2000, 0, 0)，声源到坐标原点 O 的距离 r 0 ᫼ѵᡰሏ/m 15 ࣨए/dB
为 2000 m，接收阵列阵元数为 25，阵元间距设为 0.4
20
2 m。阵元分布在 26 ∼ 74 m 深度处，倾斜阵的中 0.2
25
心参考阵元坐标为 (0, 0, 50)，垂直阵的倾斜角度为
300 400 500 600
5 。声源与倾斜阵平面构成的夹角ϕ为60 。图4(a) ᄱࠫ௑ᫎ/ms
◦
◦
是声源方位角为 60 时阵列接收到的格林函数理论 (b) ܦູவͯᝈ˞60°௑ଢԩಫ౤Ѧ஝ڏϸ
◦
值，图 4(b) 是声源方位角为 60 时通过盲反卷积提 -1.0 1.0
◦
取到的格林函数图像，图4(c) 是利用图4(b)格林函 ಫ౤Ѧ஝வͯԋሮ
0.8
数得到的波束-时间偏移图像。 -0.5
0.6
图 4(c) 前 4 个波束峰值点时间分别是 337 ms、 sinθ 0 ࣨएॆʷӑ
343 ms、353 ms、423 ms，对应阵列观测角正弦值 0.4
−0.031、0.164、−0.122、0.306。通过最小二乘方法估 0.5 0.2
计阵不变量χ t 并解算声源距离。直接利用倾斜阵进 1.0
300 400 500 600
行测距的估计结果为2911 m，相对误差为45%。 ᄱࠫ௑ᫎ/ms
通过自校正方位距离联合估计算法对阵列倾 (c) வͯᝈ˞60°௑ฉౌ-௑ᫎϠረڏϸ
角在声源 -接收平面内的投影值进行估计，估计结 图 4 阵列倾斜平面与声源成 60 夹角时格林函数
◦
果如图 5 所示，∆θ cos ϕ 的估计值为 2.5 ，经过算法 图像和波束 -时间偏移图
◦
校正后距离估计值 r 为 2171 m，相对误差降低到 Fig. 4 Green’s function and beam-time migration
8.6%，比校正前减少了 36.4%。在已知阵列倾角为 diagram when the incline angle between array in-
ˆ
∆θ 为 5 的情况下，求得方位角的估计值 ϕ 为 60 。 clined plane and sound source is 60 ◦
◦
◦
由于倾斜阵存在固有的左右舷模糊问题，此处仅考 10
虑声源方位为0 ∼ 180 之间的情况。
◦
◦
3.2 联合估计算法定位精度影响因素的定量分析 J(Dθ) 5
联合估计算法的影响因素主要包括阵列的倾
斜程度和声源的方位角，本节首先分析了阵列倾斜 0 -10 -8 -6 -4 -2 0 2 4 6 8 10
角度对测距精度的影响，随后分别研究了阵列倾斜 Dθ cosφ
角度和声源方位这两个影响因素对联合估计算法 图 5 方位角为 60 时联合自校正算法的代价函数
◦
的影响，对比处在不同倾斜角度的阵列估计来自不 Fig. 5 The cost function of self-calibrate algo-
同方位的声源位置时联合估计算法性能的优劣。 rithm at azimuth angle of 60 degrees