Page 108 - 《应用声学》2023年第6期

1218 2023 年 11 月

个调向范围，各阶数下波束形成器的主瓣期望指向
2 现有均匀插值点多项式结构设计及其问 越偏离中心位置，指向偏差越大。从图 2(b) 可以看
题分析
出，DI 的最小值位于调向范围的边缘处；并且阶数
越低，DI最小值也越低。具体来说，当M = 4 时，主
为了分析现有多项式结构设计存在的主瓣指
瓣最大指向偏差为 12.46 ，对应最小 DI 为 5.30 dB；
◦
向偏差问题，本文以基于凸优化的鲁棒设计方法为
相比之下，当M = 7 时，指向偏差最大值仅为3.92 ，
◦
例进行分析。该方法是典型的多项式结构宽带波束
对应最小DI为7.57 dB。
形成器设计方法，文献[7]首先将其运用于多项式结
构波束形成器设计中，后来又被应用于二维多项式
表 1 多项式阶数对波束形成器性能的影响
结构波束形成器设计和三角函数多项式结构波束
Table 1 Effect of polynomial order on the
形成器设计 [13−14] 。该设计方法对应的优化问题可 beamformer performance
表示为
I−1 L−1 指向偏差/(°) DI/dB
∑ ∑ 多项式阶数 M
2
min |P(ψ i , f q , θ l ) − P d (ψ i , f q , θ l )| , (7a) 最大值 平均值 最小值 平均值
w(f q ) 4 12.46 6.29 5.30 6.45
i=0 l=0
5 7.77 4.53 6.58 6.93

T
 w (f q )g(ψ i , f q , ψ i ) = 1, (7b) 6 5.00 3.02 7.14 7.31

 7 3.92 2.34 7.40 7.57
s.t. T 2
 |w (f q )g(ψ i , f q , ψ i )|
 > γ, (7c)
 2 14
T
∥w (f q ) [I K ⊗ s(D)]∥
M/
其中，i = 0, · · · , I − 1，q = 0, · · · , Q − 1，l = 12 M/
M/
0, · · · , L − 1，分别表示可调范围的插值点、频率样 10 M/
点及入射角度范围的离散点；式(7b) 为期望方向上 8
的无失真约束；式 (7c) 为 WNG 约束，γ 为 WNG 约 ૉՔϠࣀ/(°)
束的门限。 6
考虑远场条件下 K = 8 阵元组成的线阵，阵 4
元间隔 d = 0.045 m，声速 c = 340 m/s，采样 2
频率 f s = 8000 Hz，WNG 约束的门限值 γ dB =
0
40 60 80 100 120 140
−35 dB，入射角度范围 Θ = [0 , 180 ]，频率范 ូՔᝈए/(°)
◦
◦
围 Ω = [200, 3700] Hz，主瓣期望指向可调范围 (a) ૉՔϠࣀ
Ψ = [40 , 140 ]，从中均匀选取 11 个插值点，此时
◦
◦
8.0
ψ i = [40 50 60 · · · 140 ]；对于期望指向角度 ψ，
◦
◦
◦
◦
通带范围为 Θ ML = [ψ − 5 , ψ + 5 ]，阻带范围为 7.5
◦
◦
Θ SL = [0 , ψ − 35 ] ∪ [ψ + 35 , 180 ]，期望的波 7.0
◦
◦
◦
◦
束响应 P d (ψ, f, θ) 在通带范围内为 1，阻带范围内
为 0。求得滤波器频率响应 W k,m (f) 后，用抽头数 ૉՔভૉ஝/dB 6.5
N = 512 的滤波器逼近计算后的频率响应，从而获 6.0 M/
得各滤波器抽头权值。 M/
M/
5.5
表1 给出了不同多项式阶数下波束形成器的最 M/
大指向偏差与最小DI，同时也计算了整个调向范围 5.0
40 60 80 100 120 140
内指向偏差与 DI 的平均值。可以发现，随着多项式 ូՔᝈए/(°)
阶数的增加，波束形成器的指向偏差减小，DI 则随 (b) DI
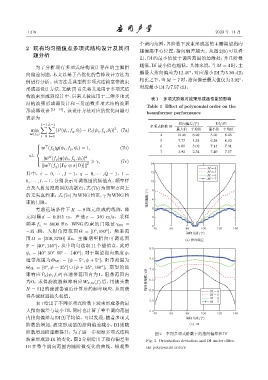
阶数增加而逐渐提升。为了进一步观察多项式结构 图 2 不同多项式阶数下的指向偏差和 DI
波束形成器 DI 的变化，图2 分别给出了指向偏差和 Fig. 2 Orientation deviation and DI under differ-
DI 在整个调向范围内随阶数变化的曲线。纵观整 ent polynomial orders