Page 51 - 《应用声学》2023年第6期

第 42 卷 第 6 期 宋云红等： 横向各向同性地层快速各向异性反演方法 1161

∫
算，将提高 VTI 各向异性反演的效率，这一方法将 +∞ 2 2
S ST (ω, V SH ) ω A (ω)dω
在下面快速 VTI 各向异性反演方法研究中进一步 ¯ −∞
S ST = ∫ , (5)
研究和探讨。 +∞ ω A (ω)dω
2
2
−∞
1200
¯
ေ᝷ᮠஙజጳ ଣϙᮠஙజጳ 式(5)中，S ST 为采用非频散方式处理斯通利波阵列
1150
V SH0 V f0 V SH0V f0 波形获得的慢度值，S ST (ω, V SH )为假设水平横波速
- -
1100 V SH V f0 V SH V f0 度为V SH 时计算频散方程得到的斯通利波理论频散
ᤴए/(mSs -1 ) 1050 V SHV f + + 曲线，A(ω)表示斯通利波频谱。也就是说，用非频散
+
+
V SHV f0
V SHV f0
-
+
V SH V f
1000
950 方式 (如波形反演法) 计算得到的波形慢度实际上
相当于其慢度频散曲线在频域加权平均的结果。根
900
据式 (5)，在利用斯通利波反演 VTI 各向异性时，首
850
0 1 2 3 4 5 6 7 8 9 10 先通过处理斯通利波阵列波形，计算得到非频散的
ᮠဋ/kHz
¯
慢度值 S ST 和声波频谱 A(ω)；然后给定水平横波速
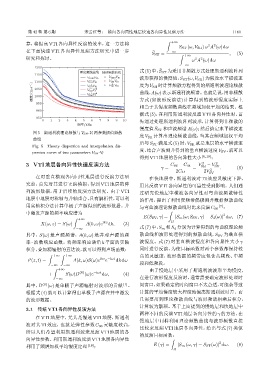
图 5 斯通利波理论频散与 V SH-V f 两参数插值频散
度 V SH 计算出理论频散曲线，当其在频域加权平均
曲线
后与S ST 满足式 (5)时，V SH 就是地层的水平横波速
¯
Fig. 5 Theory dispersion and interpolation dis-
度，结合声波测井得到的垂直横波速度V SV ，就可以
persion curve of two parameters V SH-V f
得到VTI地层的各向异性大小 [6,19] ：
2
2
3 VTI地层各向异性快速反演方法 C 66 − C 44 V SH − V SV
γ = = 2 . (6)
2C 44 2V SV
在对垂直横观各向同性地层进行反演方法研 在快地层中，斯通利波对 TI 效应灵敏度下降，
究前，首先对其进行正演模拟，得到 VTI 地层的阵 用其反演VTI各向异性的可靠性受到影响。人们通
列波形数据，用于后续的反演方法研究。由于 VTI 过研究快地层中横波各向异性对弯曲波频散特性
地层中地层对称轴与井轴重合，具有解析性，可以利 的作用，提出了利用宽频带偶极测井数据频散曲线
用实轴积分法计算单极子声源得到的波形数据。井 [7]
与弯曲波理论频散曲线对比来反演C 66 ：
中激发声源的频率响应谱为 ∫ 2
E(S SV , γ)= |S m (ω; S SV , γ) − S d (ω)| dω, (7)
∫
+∞ Ω
X(ω, z) = S(ω) A(k, ω)e ikz dk, (3)
式(7)中，S m 和S d 分别为计算得到的弯曲波理论频
−∞
其中，S(ω) 是声源频谱，A(k, ω) 是井对声源的频 散曲线和波形处理得到的频散曲线，S SV 为垂直横
率 - 波数响应函数。将频率响应谱沿 k 平面的实轴 波慢度。式 (7) 对垂直横波慢度和各向异性大小 γ
积分，叠加源辐射的直达波，就可以得到声场函数： 同时进行反演，为使目标函数对两个参数都保持较
∫ ∫
+∞ +∞ 高的灵敏度，波形数据的频带应包含高频段、中频
e
P(z, t) = A(k, ω)S(ω)e ikz −iωt dkdω
段和低频段。
−∞ −∞
∫
+∞ 由于慢地层中采用了斯通利波波形平均慢度，
+ S(ω)D (0) (ω)e −iωt dω, (4)
在进行波形慢度反演时，通常需要确定波形处理时
−∞
其中，D (0) (ω) 是单极子声源辐射对波形的贡献 [1] 。 间窗口，如果确定的时间窗口不太合适，可能会导致
根据式 (4) 就可以计算得出单极子声源在井中激发 计算的平均慢度较大程度地偏离斯通利波时差。而
的波形数据。 且需要用到理论频散曲线与波形频谱相乘后积分，
计算较为繁琐。基于上面提到的慢地层和快地层中
3.1 传统VTI各向异性反演方法
两种不同的反演 VTI 地层各向异性的 γ 的方法，在
在 VTI 地层中，尤其是慢速 VTI 地层，斯通利
慢地层中同样利用理论频散曲线与波形频散直接
波对其 TI 效应，也就是弹性参数 C 66 灵敏度较高，
比较来反演 VTI 地层各向异性，给出与式 (7) 类似
所以人们希望利用斯通利波来反演 VTI 地层的各
的反演目标函数：
向异性参数。利用斯通利波反演VTI地层各向异性 ∫
2
利用了频谱加权平均慢度定理 [18] ： E (γ) = |S m (ω, γ) − S ST (ω)| dω. (8)
Ω