Page 52 - 《应用声学》2023年第6期

1162 2023 年 11 月

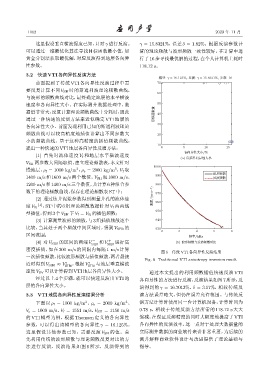
这里假设垂直横波慢度已知，只对 γ 进行反演。 γ = 15.8321%，误差 δ = 1.82%。根据反演参数计
可以通过一维最优化算法寻找目标函数最小值，如 算的理论频散与波形频散一致性较好。在计算中进
黄金分割法获取最优解，对应反演得到地层各向异 行了 16步寻找最优解的过程，在个人计算机上耗时
性参数。 118.12 s。
3.2 快速VTI各向异性反演方法
വی: γ=16.125%, Ԧ໦: γ=15.8321%, ൦஝: 16
前面提到了传统 VTI 各向异性反演过程中需 70
要反复计算不同 V SH 时的斯通利波理论频散曲线，
60
与波形的频散曲线对比，最终确定地层的水平横波
速度和各向异性大小。在实际测井数据处理中，数 50
据量非常大，反复计算理论频散曲线十分耗时，因此 ᄬಖѦ஝ϙ 40
通过一种快速的反演方法来近似确定 VTI 地层的
30
各向异性大小。前面发现利用已知的斯通利波理论
频散曲线可以较高精度地插值计算出不同参数大 20
小的频散曲线。基于这种高精度的插值频散曲线，
10
提出一种快速的VTI地层各向异性反演方法： 0 5 10 15
ՊՔपভܸ࠵/%
(1) 首先对流体速度 V f 和地层水平横波速度
(a) Ԧ໦ՊՔपভܸ࠵
V SH 两参数大间隔取值，建立理论频散表，本文针对
1000
3
3
慢地层，ρ f = 1000 kg/m ，ρ s = 2000 kg/m ，V f 取
ฉॎᮠங
1400 m/s 和 1600 m/s 两个数值，V SH 取 1000 m/s、 990 Ԧ໦ᮠங
1200 m/s 和1400 m/s三个数值，共计算6 种组合参 980
数下的理论频散曲线，保存在理论频散表ST中； 970
(2) 通过钻井泥浆参数得到测量井孔的流体速 ᤴए/(mSs -1 )
[1] ， ST 中的 6 组理论频散数据针对 V f 两两线 960
度 V f0
950
型插值，得到3个V SH 下V f = V f0 的插值频散；
(3) 计算测量波形的频散，与3组插值频散逐个 940
比较，当其处于两个频散中间区域时，得到 V SH0 的 930
2 3 4 5 6
区间范围； ᮠဋ/kHz
+
−
(4) 对 V SH0 的区间的两端 V SH0 和 V SH0 进行高 (b) ฉॎᮠஙˁԦ໦ᮠஙࠫඋ
密度插值，如在 200 m/s 的间隔内每隔 1 m/s 计算
图 6 传统 VTI 各向异性反演结果
一次插值频散，比较波形频散与插值频散，两者最接
Fig. 6 Traditional VTI anisotropy inversion result
近时得到 V SH0 ≈ V SH0 ，根据 V SH0 与地层垂直横波
′
′
速度V SV 可以计算得到VTI地层各向异性大小。 通过本文提出的利用频散插值快速反演 VTI
经过以上 4 个步骤，就可以快速反演出 VTI 地 各向异性的方法进行反演，反演结果如图7 所示，反
层的各向异性大小。 演得到的 γ = 16.7013%、δ = 3.57%，相较传统反

3.3 VTI地层各向异性反演结果分析 演方法误差略大，但仍在误差允许范围。与传统反
下面以 ρ f = 1000 kg/m 、ρ s = 2000 kg/m 、 演方法计算时使用同一台计算机设备，计算时间为
3
3
V s = 1000 m/s、V f = 1551 m/s、V SH = 1150 m/s 0.78 s，相较于传统反演方法所需的 118.12 s 大大
的 VTI 模型为例，根据 Thomsen 定义的各向异性 缩减，在保证反演精度的同时大幅度地提高了 VTI
参数，可以得出该模型的各向异性 γ = 16.125%。 各向异性的反演效率，这一点对于处理大数据量的
这里假设其他参数已知，需要反演 V SH 的值。首 实际测井数据的商业软件来讲非常重要，为后续的
先利用传统的波形频散与理论频散反复对比的方 测井解释商业软件设计与改进提供了理论基础与
法进行反演，反演结果如图 6 所示，反演得到的 指导。