Page 49 - 《应用声学》2023年第6期

第 42 卷 第 6 期 宋云红等： 横向各向同性地层快速各向异性反演方法 1159

利用误差计算公式计算理论频散与非插值频散之 对ρ s 、V f 和ρ f 分别为唯一变量的频散曲线采用
间的整体误差分别为 0.01%、0.02% 和 0.17%，最大 对称插值和非对称插值方式，计算得到的插值频
误差分别为 0.09%、0.25%和0.94%，误差非常小，在 散曲线与理论频散曲线的对比情况在图 4 中给出。
误差允许范围。通过上面的误差分析，可以看出其 图 4 可以直观地体现出插值频散曲线与理论频散曲
他参数保持不变时，无论采用对称插值还是非对称 线一致性很好，具体的误差计算结果在表 1 中给出。
插值方法，水平横波速度每隔 200 m/s 计算一次理 可以看出利用这 3 个参数对斯通利波理论频散曲线
论频散曲线，就可以高精度地插值出位于其中不同 插值计算的最大误差的最大值为 1.63%，在误差允
速度的频散曲线。 许范围。
1200 1200
ଣϙᮠஙజጳ1 ଣϙᮠஙజጳ1
1150 ଣϙᮠஙజጳ2 1150 ଣϙᮠஙజጳ2
ଣϙᮠஙజጳ3 ଣϙᮠஙజጳ3
ေ᝷ᮠஙజጳ ေ᝷ᮠஙజጳ
1100 1100
ေ᝷ᮠஙజጳ 1+- ေ᝷ᮠஙజጳ 1+-
ေ᝷ᮠஙజጳ 2+-
ေ᝷ᮠஙజጳ 2+-
ᤴए/(mSs -1 ) 1050 ေ᝷ᮠஙజጳ 3+- ᤴए/(mSs -1 ) 1050 ေ᝷ᮠஙజጳ 3+-
1000
1000
950 950

900 900

850 850
0 2 4 6 8 10 0 2 4 6 8 10
ᮠဋ/kHz ᮠဋ/kHz
(a) ࠫሦଣϙ (b) ᭤ࠫሦଣϙ

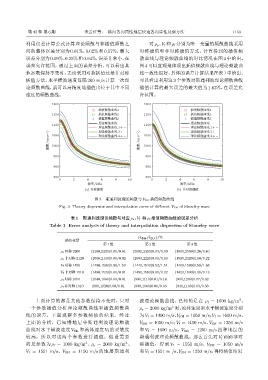
图 3 斯通利波理论频散与 V SH 插值频散曲线
Fig. 3 Theory dispersion and interpolation curve of different V SH of Stoneley wave

表 1 斯通利波理论频散与对应 ρ s、V f 和 ρ f 插值频散曲线的误差分析
Table 1 Error analysis of theory and interpolation dispersion of Stoneley wave

(δ 整体 /δ 最大 )/%
插值变量
第 1 组 第 2 组 第 3 组
ρ s 对称 2200 (2180,2220)0.00/0.01 (2080,2320)0.03/0.09 (1900,2500)0.20/0.40
ρ s 非对称 2120 (2060,2140)0.00/0.02 (2080,2220)0.01/0.03 (1980,2420)0.10/0.22
V f 对称 1490 (1480,1500)0.50/1.50 (1440,1540)0.52/1.54 (1400,1580)0.58/1.63
V f 非对称 1510 (1480,1520)0.00/0.01 (1490,1560)0.01/0.02 (1420,1600)0.08/0.13
ρ f 对称 1050 (1040,1060)0.00/0.01 (990,1110)0.01/0.14 (900,1200)0.07/0.62
ρ f 非对称 1010 (980,1020)0.00/0.01 (990,1060)0.00/0.05 (940,1160)0.03/0.33

3
上面计算的都是其他参数保持不变时，只对 波理论频散曲线，已知的是在 ρ f = 1000 kg/m 、
一个参数插值分析理论频散曲线和插值频散曲 ρ s = 2000 kg/m 时，流体速度和水平横波速度分别
3
线的误差，下面观察多参数插值的结果。经过 为V f = 1400 m/s、V SH = 1050 m/s；V f = 1600 m/s、
上面的分析，已知慢地层中斯通利波理论频散 V SH = 1050 m/s；V f = 1400 m/s、V SH = 1250 m/s
曲线对水平横波速度 V SH 和流体速度 V f 的灵敏度 和 V f = 1600 m/s、V SH = 1250 m/s 四种地层的
较高，所以对这两个参数进行插值。假设需要 斯通利波理论频散曲线。那么首先对 V f 两两非对
3
的是参数为 ρ f = 1000 kg/m 、ρ s = 2000 kg/m 、 称插值，得到 V f = 1551 m/s、V SH = 1050 m/s
3
V f = 1551 m/s、V SH = 1150 m/s 的地层斯通利 和V f = 1551 m /s、V SH = 1250 m/s，再将插值结果