Page 39 - 《应用声学》2024年第1期

第 43 卷 第 1 期 寻天雨等： 基于四水听器的充水弹性管声速测量方法 35

表 1 不同边界下实验结果分析
Table 1 Analysis of the measurement results of different boundaries
√
n 标准差 A 类标准不确定度 u A = s/ n=
1 ∑ 方差
平均值 ¯x = x i ， n v v
n
n
参数 边界 n i=1 s = 1 ∑ (x i − ¯x) 2 u 1 ∑ (x i − ¯x) 2 u 1 ∑ (x i − ¯x) 2
u
u
2
t
x i 为对应参数的测量值 n − 1 s= t n − 1 (n − 1)n
i=1 i=1 i=1
2
硬边界 1450.51 m·s −1 5.16 m ·s −2 2.27 m·s −1 0.3 m·s −1
2
声速 (c 0 ) 吸声边界 1450.14 m·s −1 2.99 m ·s −2 1.73 m·s −1 0.23 m·s −1
2
软边界 1450.40 m·s −1 3.62 m ·s −2 1.90 m·s −1 0.26 m·s −1
√
1500 壁材料密度为 ρ s ，纵波声速为 c l = (λ + 2µ)/ρ s ，
ᆶ᣸ႍ(5.26) √ µ/ρ s ，λ 和 µ 是拉密常数。圆柱
ծܦ᣸ႍ(5.27) 横波声速为 c t =
1480
ᣄ᣸ႍ(5.27)
管沿圆柱轴向坐标定义为 z，圆柱体横截面上的径
向坐标定义为 r，θ 定义为角度坐标，在声源轴对
c /(mSs -1 ) 1460 称激励下，管中声场与极角 θ 无关，忽略时间因子
1440
。设管内水中声压为 p，管壁采用位移势 Φ 和
e
−jωt
T
Ψ = (Ψ r , Ψ z , Ψ θ ) 表示纵向势标量和横向势矢量，
1420
它们均满足齐次亥姆霍兹方程，在轴对称情况下相
1400 应的解可以写为
1500 2000 2500 3000 3500 4000
f/Hz 当0 6 r 6 b时，水中声场：
( ) 2
ω
图 3 不同边界下声速测量结果 p = AJ 0 (k r r) e jk z z , k + k = . (7)
2
2
r z c
Fig. 3 Measurement results of sound velocity with
当b 6 r 6 a时，弹性管壁中的声场：
different boundaries
Φ = [BJ 0 (k lr r) + CN 0 (k lr r)] e jk z z ,
在该方法中，虽然利用每组水听器即可分离出
2
2
2
平面波入射波和反射波，同时得到边界的反射系数， k + k = (ω/c l ) , (8)
z
lr
但是考虑实际操作，每次边界悬挂时倾斜程度、位 Ψ θ = [DJ 1 (k tr r) + EN 1 (k tr r)] e jk z z ,
置等均会有差异，导致反射波会有差异，处理结果不 k + k = (ω/c t ) , (9)
2
2
2
tr
z
稳定，而入射波由声源持续发出，信号稳定，所以处
其中，k z = ω/c 0 表示轴向波数，c 0 为管内声速，k r 、
理过程采用入射波更加合理。
k lr 、k tr 表示轴向波数。
在 r = a 处，管外壁为固体 -真空自由边界，声
3 声速测量方法的验证
场满足切应力和正应力为 0 的条件，如式 (10a) 和
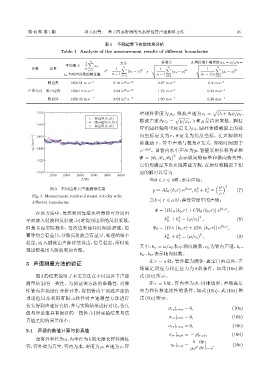
图3 的结果说明了本文方法在不同边界下声速 式 (10c)所示。
测量结果的一致性。为验证该方法的准确性，对弹 在 r = b 处，管内壁为水 -固体边界，声场满足
性管内声场进行分析计算，得到管内平面波声速的 应力和位移连续性的条件，如式 (10b)、式 (10d) 和
理论值以及利用有限元软件对声速测量方法进行 式 (10e)所示。
仿真得到声速仿真值，并与实验结果进行对比，仿真
σ rz | r=a = 0, (10a)
值与理论值具有很好的一致性，同时实验结果与仿
σ rz | r=b = 0, (10b)
真值之间的误差很小。
σ rr | r=a = 0, (10c)
3.1 声速的数值计算与仿真值
σ rr | r=b = − p| r=b , (10d)
设有外半径为a、内半径为b的无限长弹性圆柱
管，管外壁为真空，管内为水，密度为ρ，声速为 c，管 u r | r=b = 1 ∂p , (10e)
2
ρω ∂r r=b