Page 37 - 《应用声学》2024年第6期

第 43 卷 第 6 期 王晓楠等： 多项式结构恒定束宽波束形成器的高效稀疏化设计 1213

0
0 -5
-5 -10
-10
ܙᄞ/dB -15 -15
-20
-25
-30 ܙᄞ/dB -20
-35
1.0 -25
1.5
2.0 -30
2.5 150 180
3.0 90 120 -35
3.5 0 30 60 ᝈए/(O) 0 30 60 90 120 150 180
ᮠဋ/kHz
ᝈए/(O)
(a) ਫ਼ଢሪႠካข(ʼ፥ڏ) (d) ਫ਼ଢሪႠካข(Ο᜽ڏ)
0
0 -5
-5 -10
-10
ܙᄞ/dB -15 -15
-20
-25
-30 ܙᄞ/dB -20
-35
1.0 -25
1.5
2.0 -30
2.5 150 180
3.0 90 120 -35
3.5 0 30 60 ᝈए/(O) 0 30 60 90 120 150 180
ᮠဋ/kHz
ᝈए/(O)
(b) ဘదሪႠካข(ʼ፥ڏ) (e) ဘదሪႠካข(Ο᜽ڏ)
0
0 -10
-10 -20
ܙᄞ/dB -30 -30
-20
-40
-50 ܙᄞ/dB
-60 -40
1.0
1.5
2.0 -50
2.5 150 180
3.0 60 90 120 -60
3.5 0 30 ᝈए/(O) 0 30 60 90 120 150 180
ᮠဋ/kHz
ᝈए/(O)
(c) ᭤᱕ೢካข(ʼ፥ڏ) (f) ᭤᱕ೢካข(Ο᜽ڏ)
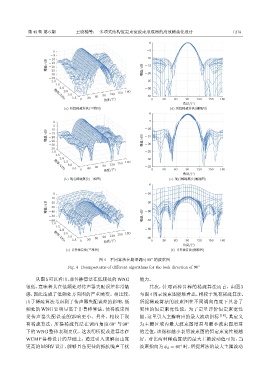
图 4 不同算法在期望调向 90 的波束图
◦
Fig. 4 Beampatterns of different algorithms for the look direction of 90 ◦

从图5可以看出，非鲁棒算法在低频处的WNG 能力。
很低，意味着其在低频处对传声器失配误差非常敏 其次，针对两种鲁棒的稀疏算法而言，由图 3
感，因此造成了低频处方向图的严重畸变。相比较， 与图 4 所示波束图能够看出，相较于现有稀疏算法，
由于稀疏算法考虑到了传声器失配误差的影响，低 所提稀疏算法的波束图在不同调向角度下具备了
频处的 WNG 要明显高于非鲁棒算法，使得波束图 更佳的恒定束宽性能。为了定量评价恒定束宽性
受传声器失配误差的影响更小。另外，相较于现 能，这里引入主瓣响应的最大波动指标 [18] ，其定义
有稀疏算法，所提稀疏算法在调向角度 60 与 90 ◦ 为主瓣区域内最大波束图增益与最小波束图增益
◦
下的 WNG 整体表现更优。这表明所提改进算法在 的差值，该指标越小表明波束图的恒定束宽性能越
WCMP 鲁棒设计的基础上，通过引入求解自由度 好。对比两种稀疏算法的最大主瓣波动值可知，当
更高的 MSRV 设计，能够具备更佳的抵抗噪声干扰 波束指向为 ϕ d = 60 时，所提算法的最大主瓣波动
◦