Page 71 - 《应用声学》2025年第2期

第 44 卷 第 2 期 李昌伟等： 应用于电气设备局部放电定位的改进相位变换加权可控响应功率算法 331

图 4 表明，在低 SNR 情况下，本文算法对单个 图 6 表明，在低 SNR 情况下，本文算法对单
指数衰减正弦信号源的定位正确率和定位 RMSE 个指数衰减 chirp 信号源的定位正确率始终高于
优于其他两种算法。当 SNR 低于 10 dB 时，本文算 其他两种算法。本文算法对单个指数衰减 chirp 信
法的定位性能提升更为明显。 号源的方位角定位 RMSE 始终小于其他两种算法，
下面对指数衰减 chirp 信号进行仿真。设置声 仰角定位 RMSE 基本与 SRP-PHAT-SCOT 算法一
源方位角为 86 ，仰角为 10 。使用三种算法分别 致。此外，三种算法对指数衰减 chirp信号的定位性
◦
◦
对某一帧 SNR 为 0 dB 的信号进行计算。对于每一 能要优于指数衰减正弦信号。
种算法的计算结果，在整个搜索空间内，根据各 在单声源定位仿真中，当SNR 在 0 ∼ 20 dB 范
搜索方向的 SRP 函数值分别绘制 SRP 谱图如图 5 围内变化时，本文算法相比于 SRP-PHAT 算法和
所示。 SRP-PHAT-SCOT 算法的定位性能平均提升效果
如表1所示。
由图 5 可以看出，传统 SRP-PHAT算法仍然会
在错误的位置产生大量谱峰，造成定位错误。SRP- 3.3 多声源定位仿真分析
PHAT-SCOT 算法的 SRP 谱图几乎不存在错误谱 在多声源定位仿真中，共设置了两个声源。首
峰，该算法能够准确定位到声源位置。SRP-PHAT- 先还是对指数衰减正弦信号进行仿真。设置第一个
RPCA 算法也能够准确定位到声源位置，其声源主 声源的方位角为 110 ，仰角为 3 ；第二个声源方位
◦
◦
瓣宽度较SRP-PHAT-SCOT算法有所增加。 角为76 ，仰角为 −3 。使用三种算法分别对某一帧
◦
◦
当 SNR 在 0 ∼20 dB 范围内变化时，三种算 SNR 为 0 dB 的信号进行计算。对于每一种算法的
法对单个指数衰减 chirp 信号源的定位性能如图 6 计算结果，在整个搜索空间内，根据各搜索方向的
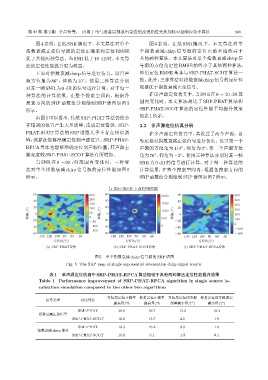
所示。 SRP函数值分别绘制SRP谱图如图7所示。

ͥᝠܦູͯᎶ ᄾࠄܦູͯᎶ
60 250 60 2000 60 600
200 500
40 40 40
150 1500 400
20 100 20 20 300
̈́ᝈ/(O) 0 50 ̈́ᝈ/(O) 0 1000 ̈́ᝈ/(O) 0 200
0
-20 -20 500 -20 100
-50
0
-40 -100 -40 0 -40
-150 -100
-60 -60 -60 -200
140 120 100 80 60 40 140 120 100 80 60 40 140 120 100 80 60 40
வͯᝈ/(O) வͯᝈ/(O) வͯᝈ/(O)
(a) SRP-PHATካข (b) SRP-PHAT-SCOTካข (c) SRP-PHAT-RPCAካข
图 5 单个指数衰减 chirp 信号源的 SRP 谱图
Fig. 5 The SRP map of single exponential attenuation chirp signal source

表 1 单声源定位仿真中 SRP-PHAT-RPCA 算法相较于其他两种算法定位性能提升效果
Table 1 Performance improvement of SRP-PHAT-RPCA algorithm in single source lo-
calization simulation compared to the other two algorithms

方位角定位正确率 仰角定位正确率 方位角定位均方根 仰角定位均方根误差
信号类型 对比算法
◦
◦
提高量/% 提高量/% 误差减小量/( ) 减小量/( )
SRP-PHAT 38.8 36.7 13.2 10.3
指数衰减正弦信号
SRP-PHAT-SCOT 18.5 15.7 2.5 1.9
SRP-PHAT 18.3 16.2 3.9 1.9
指数衰减 chirp 信号
SRP-PHAT-SCOT 10.2 6.1 1.3 0.1