Page 182 - 《应用声学》2025年第3期

716 2025 年 5 月

令 M = H 11 − H 21 ，N = H 12 − H 22 ，O = 1000
H 13 − H 23 ，P = H 31 − H 41 ，R = H 32 − H 42 ，S =
2
H 33 − H 43 ，引入T = σ 1 /w 1 = (ρ 1 c /p 1 ) tan(kp 1 d) 800
来关联流固耦合界面处的法向应力和法向位移，以
消去法向应力得到 ᄱᤴए/(mSs -1 )
 600
Mu 1 + (N + TO) w 1 = 0,

(11)
Pu 1 + (R + TS) w 1 = 0,

400
其中，c、ρ 1 和d为流体层的声速、密度和厚度。
10 20 30 40 50
方程存在非零解的充要条件是系数行列式为 ᮠဋ/Hz
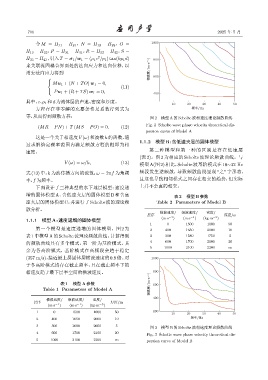
零，从而得到频散方程： 图 2 模型 A 的 Scholte 波相速度理论频散曲线
Fig. 2 Scholte wave phase velocity theoretical dis-
(MR − PN) + T (MS − PO) = 0. (12)
persion curve of Model A
这是一个关于相速度 V (ω)和波数k 的函数，通
1.1.2 模型B：含低速夹层的固体模型
过求解给定频率范围内满足频散方程的根即为相
速度， 第二种模型和第一种的区别是存在低速层
(表 2)。图 3 为相应的 Scholte 波理论频散曲线。与
V (ω) = ω/k, (13)
模型 A(图 2) 相比，Scholte 波基阶模式在 10∼32 Hz
式(13) 中，k 为波传播方向的波数；ω = 2πf 为角频 频段发生逆频散，导致频散曲线呈现 “之” 字形态，
率，f 为频率。 且这也导致相邻模式之间存在相交的趋势，但实际
下面设计了三种典型的水下地层模型：速度递 上并不会真的相交。
增的固体模型 A、含低速夹层的固体模型 B 和含高 表 2 模型 B 参数
速夹层的固体模型C，并进行了Scholte波的理论频 Table 2 Parameters of Model B
散分析。
横波速度/ 纵波速度/ 密度/
层序 厚度/m
1.1.1 模型A：速度递增的固体模型 (m·s −1 ) (m·s −1 ) (kg·m −3 )
1 0 1500 1000 50
第一个模型是速度递增的固体模型。图 2 为 2 400 1650 2000 10
表 1中模型A的Scholte波理论频散曲线。计算得到 3 200 1580 1750 5
的频散曲线具有多个模式，第一阶为基阶模式，其 4 600 1700 2100 20
5 1000 2100 2200 ∞
余为各高阶模式，基阶模式在高频段会趋于稳定
(357 m/s)，接近最上层固体层横波速度的0.9倍。对 1000
于各高阶模式均存在截止频率，且在截止频率下的
相速度趋于最下层半空间的横波速度。 800
ᄱᤴए/(mSs -1 ) 600
表 1 模型 A 参数
Table 1 Parameters of Model A
400
横波速度/ 纵波速度/ 密度/
层序 厚度/m
(m·s −1 ) (m·s −1 ) (kg·m −3 )
1 0 1500 1000 50 200
10 20 30 40 50
2 400 1650 2000 10 ᮠဋ/Hz
3 500 1680 2050 5
图 3 模型 B 的 Scholte 波相速度理论频散曲线
4 600 1700 2100 20 Fig. 3 Scholte wave phase velocity theoretical dis-
5 1000 2100 2200 ∞ persion curve of Model B