Page 185 - 《应用声学》2025年第3期

第 44 卷 第 3 期 郭望等： 利用流固界面 Scholte 波的地层横波速度反演方法 719

1.0 索方法进行最优化。随着迭代次数变化，自适应获
取优化步长从而提高了反演效率，再将得到的反演
0.5
结果作为第二个阶段反演的初始模型；第二阶段加
入利用 Kuhn-Munkres 算法匹配到准确的高阶模态
ࣨϙ 0
信息进行反演。目标函数的变化如图 11(a) 所示，
-0.5

-1.0 100
0 0.1 0.2 0.3 0.4
௑ᫎ/s
௑ᫎ/ms
(a) ܦູ௑۫ฉॎ 200
1.0 300

0.8
400
0.6
ࣨϙ 500 0 5 10 15 20
0.4 ᥋஝
(a) Ռੇܳ᥋Scholteฉᝮै
0.2
Ռੇᮠங஝૶ ေ᝷ᮠஙజጳ
1000
0
0 20 40 60
ᮠဋ/Hz
(b) ܦູᮠ៨ 800
ᄱᤴए/(mSs -1 )
图 7 声源时域波形与频谱
Fig. 7 Sound source time domain waveform and 600
spectrum
2.1 模型A：速度递增的固体模型 400

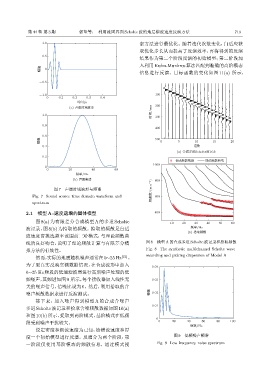
图 8(a) 为有限差分合成模型 A 的多道 Scholte 10 20 30 40 50 60
波记录，图 8(b) 为拾取的频散。拾取的频散是自适 ᮠဋ/Hz
(b) ૅԩᮠங
应速度窗挑选频率范围前三阶模式，与理论频散曲
线的良好吻合，说明了理论频散计算与有限差分模 图 8 模型 A 的合成多道 Scholte 波记录和拾取频散
拟方法的有效性。 Fig. 8 The synthetic multichannel Scholte wave
recording and picking dispersion of Model A
然而，实际的地震随机噪声通常在0∼25 Hz [22] 。
为了更真实反映实测数据情况，在合成波形中加入 0.04
0∼25 Hz频段的低通滤波器进行高斯噪声处理的低
频噪声，其频谱如图9 所示，每个接收器加入线性无 0.03
关的噪声信号，信噪比设为 6。然后，利用拾取的含
噪声频散数据来进行反演测试。 ࣨϙ 0.02
接下来，加入噪声得到模型 A 的合成含噪声
0.01
多道 Scholte波记录和拾取含噪频散数据如图10(a)
和图 10(b) 所示，提取到两阶模式，基阶模式在低频
0
段受到噪声干扰较大。 0 20 40 60 80 100
ᮠဋ/Hz
设定密度和纵波速度为已知，给横波速度和厚
度一个初始模型进行反演。反演分为两个阶段：第 图 9 低频噪声频谱
一阶段仅使用基阶模态的频散信息，通过模式搜 Fig. 9 Low frequency noise spectrum