Page 187 - 《应用声学》2025年第3期

第 44 卷 第 3 期 郭望等： 利用流固界面 Scholte 波的地层横波速度反演方法 721

Ռੇᮠங஝૶ ေ᝷ᮠஙజጳ
1000 50

60
800
ᄱᤴए/(mSs -1 ) 600 ງए/m 70 ᄾࠄവی

80
Ѻݽവی
Ԧ໦ፇ౧
400 ኄʷ᫽඀
90
ኄ̄᫽඀
Ԧ໦ፇ౧
200 100
10 20 30 40 50 0 500 1000
ᮠဋ/Hz ഷฉᤴए/(mSs -1 )
(a) ᮠங஝૶ (b) Ԧ໦ፇ౧
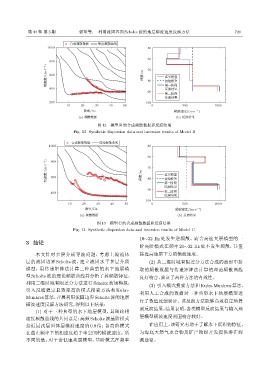
图 12 模型 B 的合成频散数据和反演结果
Fig. 12 Synthetic dispersion data and inversion results of Model B

Ռੇᮠங஝૶ ေ᝷ᮠஙజጳ
1000 50

60
ᄱᤴए/(mSs -1 ) 600 ງए/m 70 ᄾࠄവی
800

Ѻݽവی
80
ኄʷ᫽඀
Ԧ໦ፇ౧
90
400 ኄ̄᫽඀
Ԧ໦ፇ౧
100
10 20 30 40 50 0 500 1000
ᮠဋ/Hz ഷฉᤴए/(mSs -1 )
(a) ᮠங஝૶ (b) Ԧ໦ፇ౧
图 13 模型 C 的合成频散数据和反演结果
Fig. 13 Synthetic dispersion data and inversion results of Model C
10∼32 Hz 处发生逆频散。而含高速夹层模型的一
3 结论
阶高阶模式在频率 20∼32 Hz 处不发生频散，其值
本文针对多层介质导波问题，考虑上覆流体 接近高速层下方的横波速度。
层的流固边界 Scholte 波，建立流固水平多层介质 (2) 从二维时域有限差分方法合成的波形中拾
模型，用传递矩阵法计算三种典型的水下地层模 取的频散数据与传递矩阵法计算的理论频散曲线
型Scholte波的理论频散曲线并分析了其频散特征， 良好吻合，验证了两种方法的有效性。
利用二维时域有限差分方法进行 Scholte 波场模拟，
(3) 引入模式搜索方法和 Kuhn-Munkres 算法，
引入反演稳定且效率高的模式搜索方法和 Kuhn-
利用人工合成的数据对三种典型水下地层模型进
Munkres算法，开展利用流固边界Scholte波的地层
行了数值反演验证。该反演方法能够高效稳定地得
横波速度反演方法研究，得到以下结果：
到反演结果，结果表明，各类模型反演结果与输入地
(1) 对于三种典型的水下地层模型，其理论相
速度频散曲线的共同点是：高频Scholte波基阶模式 层模型横波速度剖面吻合较好。
接近最浅层固体层横波速度的 0.9 倍；各高阶模式 在应用上，该研究有助于了解水下沉积物特征、
在截止频率下的相速度趋于半空间的横波速度。所 为海底天然气水合物及矿产勘探开发提供潜在探
不同的是，对于含低速夹层模型，基阶模式在频率 测途径。