Page 183 - 《应用声学》2025年第3期

第 44 卷 第 3 期 郭望等： 利用流固界面 Scholte 波的地层横波速度反演方法 717

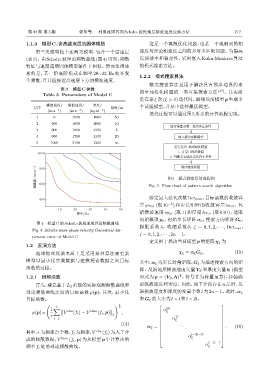
1.1.3 模型C：含高速夹层的固体模型 这是一个离散优化问题，也是一个观测到的相
第三类模型较上述两类模型，包含一个高速层 速度与理论相速度之间的多对多匹配问题。为提高
(表3)。由Scholte波理论频散曲线(图4) 可知，频散 反演效率和稳定性，采用嵌入 Kuhn-Munkres 算法
特征与速度递增固体模型条件下相似。然而值得注 的模式搜索方法。
意的是，其一阶高阶模式在频率 20∼32 Hz 处不发
1.2.2 模式搜索算法
生频散，且其值接近高速层下方的横波速度。
模式搜索算法是用于解决具有简单边界约束
表 3 模型 C 参数 的全局优化问题的一类直接搜索方法 [17] 。其实质
Table 3 Parameters of Model C
是在第 ξ 次 (ξ > 0) 迭代时，围绕当前模型 p 生成多
横波速度/ 纵波速度/ 密度/ 个试验模型，并从中选择最优模型。
层序 厚度/m
(m·s −1 ) (m·s −1 ) (kg·m −3 )
迭代过程可以通过图5所示的计算流程实现。
1 0 1500 1000 50
2 400 1650 2000 10
ፌࠀവیԠ஝njᤖ̽ጼൣ౎͈
3 800 1800 2150 5
4 600 1700 2100 20 ҫК੸үఞழവی
5 1000 2100 2200 ∞
ᤉᛡᤖ̽ ੽҂త͖വی
1000 1. ᝠካᄬಖѦ஝ϙ
2. Ѽல௧ա໘ᡜᤖ̽ጼൣ౎͈

ᣥѣత͖വی
ᄱᤴए/(mSs -1 ) 800 Fig. 5 Flow chart of pattern search algorithm
模式搜索算法流程图
图 5
600

给定最大迭代次数Iter max ，目标函数的收敛容
400
差 φ Tol (取 10 −5 ) 和步长矩阵的收敛容差 α Tol ，包
10 20 30 40 50
ᮠဋ/Hz 括横波速度 v Tol (取.1) 和厚度 h Tol (取 0.01)，选取
初始模型 p 0 ，初始步长矩阵 α 0 ，搜索方向矩阵 G 0 ，
图 4 模型 C 的 Scholte 波相速度理论频散曲线
膨胀系数 λ，收缩系数 θ，ξ = 0, 1, 2, · · · , Iter max ，
Fig. 4 Scholte wave phase velocity theoretical dis-
j = 0, 1, 2, · · · , 2n − 1。
persion curve of Model C
定义用于扰动当前模型p的矩阵χ ξ 为
1.2 反演方法

地球物理反演本质上是采用某种算法来更新 χ ξ = α ξ G ξ , (15)
模型以最小化实测数据与建模理论数据之间目标 其中，α ξ 为步长对角矩阵，G ξ 为描述搜索方向的矩
函数的过程。 阵。反演地层横波速度矢量V S 和厚度矢量 h (模型
T
1.2.1 目标函数 形式为 p = (V S , h) ，符号 T 为转置运算)，经验确
首先，建立基于L 2 范数的实际观测频散曲线和 定纵波速度和密度。因此，地下介质存在n 层时，反
理论频散曲线之间的目标函数 φ(p)；其次，最小化 演横波速度和厚度的变量个数l 为2n − 1。此时，α ξ
目标函数。 和G ξ 的大小为l × l 和l × 2l。
( ) 1  
r 2
1 ∑
obs theo
α 00
φ(p)=
V (f i ) − V (f i , p)
,  ξ 
r 2  11 
i=1  α ξ 
(14)  . . 


α ξ =  .  . (16)
其中，r 为频率点个数，f i 为频率，V obs (f i )为人工合  l−2l−2 


 α ξ 
成的频散数据，V theo (f i , p) 为从模型 p 中计算出的  
α l−1l−1
频率f i 处的理论频散曲线。 ξ