Page 202 - 《应用声学》2025年第3期

736 2025 年 5 月

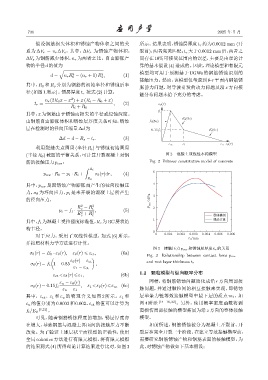
假设钢筋损失体积和锈蚀产物体积之间的关 所示。结果表明，锈蚀层厚度t r 约为0.0012 mm (开
系为 ∆V r = n r ∆V s ，其中，∆V r 为锈蚀产物体积， 裂前)，两者完美匹配；t r 大于0.0012 mm后，两者之
∆V s 为钢筋减少体积，n r 为两者之比。自由膨胀产 间存在 10% 可接受范围内的误差，主要是由理论计
物的半径d的值为 算的基本假设(4) 造成的。因此，理论模型和有限元
√ 模型均可用于预测基于 UGWs 的钢筋锈蚀识别的
2
2
d = n r R − (n r + 1) R , (1)
0 s
接触压力。然而，该模型仅考虑到θ-r 平面内钢筋锈
其中，R 0 和 R s 分别为钢筋的初始半径和锈蚀后半
胀静力问题，对导波引发的动力问题及沿 z 方向接
径(如图1所示)。锈层厚度t r 按式(2)计算：
触分布问题未给予充分的考虑。
2
n r (2R 0 x − x ) + x (R i − R 0 + x)
t r = , (2) σ θ (r)
R i + R 0
f t
其中，x 为钢筋由于锈蚀而损失的半径或侵蚀深度。
र(6b)
由钢筋自由膨胀体积和锈蚀层厚度关系可知，锈蚀 र(6a)
层在检测时的径向压缩量∆d为
0.15f t र(6c)
∆d = d − R s − t r . (3)
ε ct ε  ε u ε θ (r)
利用裂缝尖点圆周 (半径 R i ) 与锈蚀初始圆周
(半径 R 0 ) 截面的平衡关系，可计算开裂混凝土对钢 图 2 混凝土双线性本构模型
筋的接触压力p cor ： Fig. 2 Bilinear constitutive model of concrete
∫
R i
p cor · R 0 = p i · R i + σ θ (r)dr, (4) 5
R 0
其中，p cor 是因锈蚀产物膨胀而产生的径向接触压 4
力，σ θ 为环向应力，p i 是未开裂的混凝土层所产生 3
的径向压力， P cor/MPa
2
R − R 2 i 2
c
p i = f t · 2 , (5)
2
R + R
c i ஝ϙവલ
其中，f t 为混凝土受拉强度标准值，R c 为RC层状结 1 ေ᝷ᝠካ
构半径。
0
对于应力，采用了双线性模型，如式 (6) 所示， 0 0.001 0.002 0.003 0.004 0.005 0.006
t r /mm
并按照材料力学方法进行计算。
图 3 接触压力 p cor 和锈蚀层厚度 t r 的关系
σ θ (r) = E 0 · ε θ (r), ε θ (r) 6 ε ct , (6a)
Fig. 3 Relationship between contact force p cor
( )
ε θ (r) − ε ct
σ θ (r)= f t 1 − 0.85 , and rust layer thickness t r
ε 1 − ε ct
1.2 颗粒模型与纵向概率分布
ε ct <ε θ (r)6ε 1 , (6b)
ε u − ε θ (r) 同样，将钢筋锈蚀问题简化成沿 r 方向局部接
σ θ (r)= 0.15f t , ε 1 <ε θ (r)6ε u , (6c) 触问题，并通过颗粒间的相互接触来实现，即锈蚀
ε u − ε 1
其中，ε ct 、ε 1 和 ε u 的物理含义如图 2 所示。ε 1 和 层单条力链等效接触模型中最下层的质点 m 1 ，如
ε u 的值分别为 0.0003 和 0.002，ε ct 的值可以计算为 图 4 所示 [14−16,22] 。另外，使用概率密度函数将剥
[3,21] 。 离损伤局部接触的模型拓展为沿z 方向的整体接触
f t /E 0
可见，随着钢筋锈蚀程度的增加，锈层厚度亦 模型。
在增大，导致钢筋与混凝土界面间的接触压力不断 如前所述，钢筋锈蚀被分为混凝土开裂前、开
改变。为了验证上述层状平面模型的正确性，使用 裂后和完全开裂三个阶段。在建立等效接触模型前，
全局 cohesive 方法进行有限元模拟，将有限元模拟 需要研究钢筋锈蚀产物和钢筋表面的接触模型，为
的结果同式 (4) 所得理论计算结果进行比对，如图 3 此，对锈蚀产物做如下基本假设：