Page 212 - 应用声学2019年第4期

672 2019 年 7 月

ˆ
−40 dB，并且谱峰很尖锐，测向角度为 θ 1 = −1 , 复杂度的同时，能够对两个角度间隔较小的目标进
◦
ˆ
θ 2 = 25 。因此，低复杂度 MUSIC 算法测向精度高 行准确的测向。由于ESPRIT算法不需要进行谱峰
◦
于MUSIC算法。 搜索，因此无法绘制功率谱图。利用 ESPRIT 算法
0 对水池实验所获得的数据进行处理，所得到的测向
-5 结果如表 1 所示。低复杂度 ESPRIT 算法的测向精
-10
度受两目标角度间隔的影响较小，均方根误差均达
ॆʷӑҪဋ៨/dB -20 MUSIC 到了 1 ，而 ESPRIT 算法的测向性能，随着两目标
-15
Ͱܭాए
◦
MUSIC
角度间隔的减小而降低。从表1 可以看出，ESPRIT
-25
-30
杂度 ESPRIT 算法的测向精度高于 ESPRIT 算法。
-35 算法的水池实验结果与仿真实验的结果一致，低复
-40
水池实验和仿真结果都验证了低复杂度算法的有
-45
-100-80 -60 -40 -20 0 20 40 60 80 100 效性。
ᝈए/(O)
0
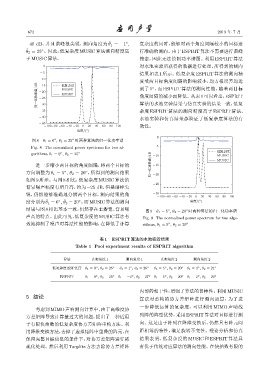
图 8 θ 1 = 0 , θ 2 = 25 时两种算法的归一化功率谱
◦
◦
Fig. 8 The normalized power spectrum for two al- -5
Ͱܭాए
◦
gorithms，θ 1 = 0 , θ 2 = 25 ◦ -10 MUSIC
进一步缩小两目标的角度间隔，将两个目标的 ॆʷӑҪဋ៨/dB -15 MUSIC
方向调整为 θ 1 = 5 , θ 2 = 20 ，所得到的测向结果 -20
◦
◦
如图 9 所示。与图 8 相比，低复杂度 MUSIC 算法的
-25
背景噪声幅度有所升高，约为 −25 dB，但是谱峰尖
锐，仍然能够准确地分辨两个目标，测向结果的角 -30
-100-80 -60 -40 -20 0 20 40 60 80 100
ˆ
◦ ˆ
度分别为θ 1 = 6 , θ 2 = 20 。而MUSIC算法的测向 ᝈए/(O)
◦
结果与图 8相比基本一致，仍然存在主瓣宽、背景噪 图 9 θ 1 = 5 , θ 2 = 20 时两种算法的归一化功率谱
◦
◦
声高的特点。由此可见，低复杂度的MUSIC算法有 Fig. 9 The normalized power spectrum for two algo-
效地抑制了噪声对算法性能的影响，在降低了计算 rithms, θ 1 = 5 , θ 2 = 20 ◦
◦
表 1 ESPRIT 算法的水池实验结果
Table 1 Pool experiment results of ESPRIT algorithm

算法 真实角度 1 测向角度 1 真实角度 2 测向角度 2

低复杂度 ESPRIT θ 1 = 0 , θ 2 = 25 ◦ θ 1 = 1 , θ 2 = 26 ◦ θ 1 = 5 , θ 2 = 20 ◦ θ 1 = 4 , θ 2 = 21 ◦
◦
◦
◦
◦
ESPRIT θ 1 = 0 , θ 2 = 25 ◦ θ 1 = −2 , θ 2 = 27 ◦ θ 1 = 5 , θ 2 = 20 ◦ θ 1 = 2 , θ 2 = 22 ◦
◦
◦
◦
◦
内部的相干性，增强了算法的鲁棒性。利用MUSIC
5 结论
算法对重构的协方差矩阵进行测向运算，为了进
一步降低运算的复杂度，可以利用 MIMO 声呐线
考虑到 MIMO声呐测向计算中，由于高维度协
方差矩阵导致计算量过大的问题，提出了一种适用 列阵的阵型优势，采用 ESPRIT 算法对目标进行测
于有限快拍数的低复杂度协方差矩阵重构方法。利 向。这是由于阵列在降维变换后，仍然具有阵元间
用降维变换方法，去掉了虚拟矩阵中重叠的阵元，在 距相等的特性，满足旋转不变性。理论分析和仿真
保留完整目标信息的条件下，对协方差矩阵进行稀 结果表明，低复杂度的 MUSIC 和 ESPRIT 算法具
疏化处理。然后利用 Toeplitz 方法去除协方差矩阵 有优于传统对应算法的测向性能。在快拍数有限的