Page 76 - 应用声学2019年第4期

536 2019 年 7 月

式 (29) 中，G = C 1 + C 2 。最后，基于 Hermitian 矩 −5 dB 和 −10 dB 时估计目标方位，但当 SNR 降
阵R 的MVDR空间谱为 低到 −15 dB 时，PV -PV -EVR 也无法估计方位。
1 相比较而言，P-V c -EVR、P-(V r + V ϕ )-EVR 两种
P MVDR = , (30)
˜ a(θ)R −1 ˜ a(θ) 方法均可以有效地消除各向同性噪声，具有较
式 (30) 中， ˜ a(θ) = [I d , 0 d×(2N+1−d) ]˜ a(θ)，θ 为扫描 ˙ ˙
强的噪声抑制能力。由于 R P -(V r +V ϕ ) − R P -V c =
˙ ˙
角度。 AR s (2I H − Φ c )A ˙ H > 0 H ， 在 低 信 噪 比 时 P-
(V r + V ϕ )-EVR 比 P-V c -EVR 具有更低的旁瓣和较
4 仿真计算结果 高的谱峰。因此，利用P-(V r + V ϕ )构造的互协方差

矩阵相比其他方法构造的协方差矩阵更适合弱目
本节通过仿真计算来验证该方法的方位估
标的方位估计。
计性能。 假设接收阵列为 8 元声矢量圆阵， 半
径为 0.35 m，声矢量传感器的振速方向分别沿
4.2 基于P -(V r + V ϕ )的不同解相干方法
着 圆 阵 的 径 向 和 切 向； 两 宽 带 相 干 信 号 s 1 (t)、
4.2.1 空间谱对比分析
s 2 (t) = βs 1 (t) (β = e jπ/5 ) 为零均值的、带宽为
假设两个相干信号分别从 100 和 160 入射
◦
◦
BW ∈ [0.5 kHz, 2.5 kHz] 的高斯信号；声源和声矢
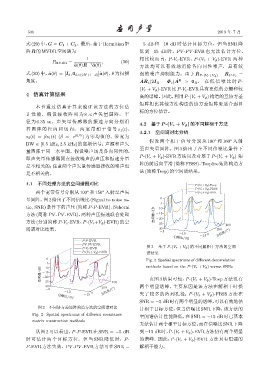
至声矢量圆阵。图 3 给出了在不同信噪比条件下
量圆阵于同一水平面。假设噪声场是各向同性的，
P-(V r + V ϕ )-EVR 方法以及对基于 P-(V r + V ϕ ) 矩
即声矢量传感器同点接收噪声的声压和振速分量
阵的前后向平滑 (简称 FBSS)、Teoplize矩阵构造方
是不相关的；任意两个声矢量传感器接收的噪声也
法(简称Teop)的空间谱结果。
是不相关的。
4.1 不同处理方法的空间谱图对比 P-(V r +V φ )-Toep
P-(V r +V φ )-FBSS
两个宽带信号分别从 100 和 150 入射至声矢 P-(V r +V φ )-EVR
◦
◦
量圆阵。图2给出了不同信噪比(Signal to noise ra- 0
-5
tio, SNR) 条件下的声压 (简称 P-P-EVR)、Nehorai -10
方法 (简称 PV -PV -EVR)、两种声压振速联合处理 ቇᫎ៨/dB -15
方法 (分别简称 P-V c -EVR、P-(V r +V ϕ )-EVR) 的空 -20
-25
400
间谱对比结果。 -30 200
-5
-10 0 வͯᝈ/(°)
-15
η٪උ/dB
P-P-EVR
PV-PV-EVR
P-V c -EVR 图 3 基于 P-(V r + V ϕ) 的不同解相干方法的空间
P-(V r +V φ )-EVR 谱结果
0
Fig. 3 Spatial spectrums of different decorrelation
-5
methods based on the P-(V r + V ϕ) versus SNRs
-10
ቇᫎ៨/dB -15 由图 3 结果可知，P-(V r + V ϕ )-Toep 方法没有
-20
-25
-30 200 400 两个明显谱峰，主要原因是该方法在解相干时损
-5
-10 0 வͯᝈ/(°)
-15 失了较多的阵列孔径；P-(V r + V ϕ )-FBSS 方法在
η٪උ/dB
SNR = −5 dB时有两个明显的谱峰，可以有效地估
图 2 不同协方差矩阵构造方法的空间谱对比 计相干目标方位，但当信噪比 SNR 下降，该方法的
Fig. 2 Spatial spectrums of different covariance
空间谱估计性能降低，在 SNR = −15 dB 时已基本
matrix construction methods
无法估计两个相干目标方位；而在信噪比 SNR下降
从图 2 可以看出，P-P-EVR 在 SNR = −5 dB 到−15 dB时，P-(V r + V ϕ )-EVR方法仍有两个明显
时可估计两个目标方位，但当 SNR 降低时，P- 的谱峰。因此，P-(V r + V ϕ )-EVR 方法具有更强的

P-EVR 方法失效。PV -PV -EVR 方法可在 SNR = 解相干能力。