Page 137 - 《应用声学》2020年第4期

第 39 卷 第 4 期 陈立等： 四阶带通箱的自回归滑动平均模型 623

18 0.05
ࠄ฾ϙ SS
SS ARMA
16
ARMA 0.04
14 0.03
᫾ઈ/W 12 ႃื/A

0.02
10
0.01
8
6 0
10 20 50 100 200 500 1000 2000 0 10 20 30 40 50 60 70 80 90 100
ᮠဋ/Hz ᧔ನག஝

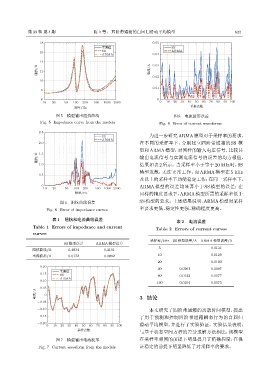
图 5 模型输出阻抗曲线 图 8 电流波形误差
Fig. 5 Impedance curve from the models Fig. 8 Error of current waveforms

2.5
SS 为进一步研究 ARMA模型对于采样率的要求，
ARMA
2.0 在不同的采样率下，分别建立四阶带通箱的 SS 模
型和 ARMA 模型，对同样的输入电压信号，比较其
1.5
᫾ઈ/W 输出电流信号与实测电流信号的误差的均方根值，
1.0 结果如表 2 所示。当采样率小于等于 20 kHz 时，SS
模型发散，无法正常工作，而 ARMA 模型在 5 kHz
0.5
及以上的采样率下均能稳定工作；在同一采样率下，
0 ARMA 模型的误差均显著小于 SS 模型的误差；在
10 20 50 100 200 500 1000 2000
ᮠဋ/Hz 同样的精度要求下，ARMA模型所需的采样率低于

图 6 阻抗曲线误差 SS模型的要求。上述结果说明，ARMA模型对采样
Fig. 6 Error of impedance curves 率要求更低、稳定性更强、精确程度更高。
表 1 阻抗和电流曲线误差
表 2 电流误差
Table 1 Errors of impedance and current Table 2 Errors of current curves
curves
采样率/kHz SS 模型误差/A ARMA 模型误差/A
SS 模型误差 ARMA 模型误差
5 0.0131
阻抗曲线/Ω 0.4834 0.2101
电流波形/A 0.0172 0.0092 10 0.0129
20 0.0103
0.20
40 0.0261 0.0087
ࠄ฾ϙ
0.15
SS 80 0.0142 0.0077
ARMA
0.10
160 0.0104 0.0075
0.05
ႃื/A 0 3 结论
-0.05
本文研究了四阶带通箱的离散时间模型，提出
-0.10
-0.15
了用于预测和控制四阶带通箱瞬态行为的自回归
-0.20
0 10 20 30 40 50 60 70 80 90 100 滑动平均模型，并进行了实验验证。实验结果表明，
᧔ನག஝
与基于状态空间方程的差分求解方法相比，该模型
图 7 模型输出电流波形 在采样率相同的前提下明显提升了精确程度，在保
Fig. 7 Current waveform from the models 证稳定的前提下明显降低了对采样率的要求。