Page 40 - 《应用声学》2020年第6期

834 2020 年 11 月

但是实际情况中累加 warping变换得到的增益往往 取值，红色虚线是理论值。可以看出每个时刻 ˜α 的
小于这个理论计算值。 提取值与真实值比较接近，因为实际噪声的影响会
若实际情况中目标方位未知且假定目标所在 导致 ˜α 存在一定的偏差。
波束不变，还可以将式 (13) 的代价函数改为对该段
0
时间初始距离与径向速度比值和目标方位的联合
-0.5
匹配：
{ }
ω 2 r=r 2 -1.0
∑ ∑

Λ(θ, ˜α) = max ˜ γ(ω, r, θ, ˜α) . (15)
˜ α,θ ࣨए/dB -1.5
ω=ω 1 r=r 1
综上，利用 warping 变换频谱累加对目标信号 -2.0
相干简正波特征频率实现增强的过程如下： -2.5
(1) 对阵列接收信号进行常规波束形成，得到
-3.0
目标方位角； 0 50 100 150 200
ᝈए/(°)
(2) 对某段距离下目标方位处的波束输出信号
(a) CBF
自相关函数进行带参数的 ˜α-warping 变换 (假定距
9.0 1.0
离与径向速度)，对变换后频谱进行求和，得到不同 0.9
8.5
˜ α 参数下式 (13) 代价函数的分布，根据代价函数的 0.8
8.0 0.7
分布得到距离与径向速度的比值； 7.5 0.6
(3) 提取最优 ˜α 值时对应的波束输出信号自相 ᡰሏ/km 0.5
关函数经 warping变换频谱累加后的高信噪比的输 7.0 0.4
6.5 0.3
出信号。
6.0 0.2
在目标方位未知的情况下，对每一扫描角度 0.1
5.5
和每一假定 ˜α 计算式 (15) 的代价函数，代价函数在 0 10 20 30 40 50 60
(θ, ˜α) 平面极大值的位置作为目标方位以及运动参 ᮠဋ/Hz
(b) warpingԫ૱ᄊᮠ៨༙࣋ڏ
数的估计。
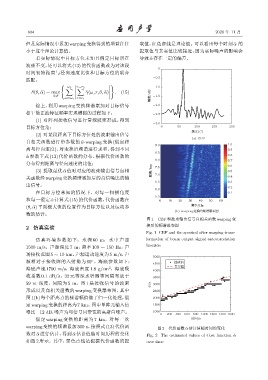
图 1 CBF 和波束输出信号自相关函数 warping 变
2 仿真实验 换后的频谱瀑布图
Fig. 1 CBF and the spectral after warping trans-
仿真环境参数如下：水深 60 m，水中声速 formation of beam output signal autocorrelation
1500 m/s。声源深度 7 m，频率 100 ∼ 150 Hz，声 function
场接收范围 5 ∼ 10 km，声源运动速度为 5 m/s，声
5000
源相对于接收阵的入射角为 60 。海底参数如下： ଢԩϙ
◦
4500
3
海底声速 1700 m/s，海底密度 1.8 g/cm ，海底吸 4000 ᄾࠄϙ
收系数 0.1 dB/λ。32 元等深水听器等间隔布放于 3500
59 m 深度，间隔为 5 m。图 1 是接收信号的波束 α⊳s ∼ 3000
形成以及自相关函数的 warping 变换瀑布图，其中 2500
图 1(b) 每个距离点的频谱幅值做了归一化处理，假 2000
定warping变换的距离为7 km。图中单阵元输入信 1500
噪比−12 dB，噪声为与信号同带宽的高斯白噪声。 1000 0 200 400 600 800 1000 1200 1400 1600
假定 warping 变换的距离为 7 km，对每一次 ௑ᫎ/s
warping 变换的频谱累加 300 s，按照式 (13) 代价函 图 2 代价函数 ˜α 估计值随时间的变化
数对 ˜α 进行估计，得到 ˜α 估计值随时间历程的变化 Fig. 2 The estimated values of Cost function ˜α
如图 2 所示。其中，黑色点线是根据代价函数的提 over time