Page 42 - 《应用声学》2020年第6期

836 2020 年 11 月

接下来说明累加warping变换对干涉简正波进 进行验证，声源能量集中在50 ∼ 350 Hz。实验海区
行相干累加的原理。图 4(a) 和图 4(b) 分别是单拍 水深约 30 m，接收阵由 48 元座底阵组成，其中有效
warping变换与单拍 ˜α-warping变换的对比图，假定 阵元个数为43个，阵元间距1.5 m左右。
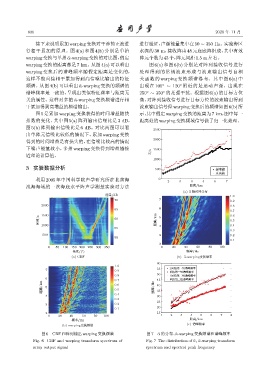
warping变换的距离都是7 km。从图 4(a)可以看出 图 6(a) 和图 6(b) 分别是对阵列接收信号进行
warping 变换后的谱峰频率随假定距离是变化的， 处理得到的常规波束形成与波束输出信号自相
这样不能直接相干累加得到高信噪比输出的特征 关函数的 warping 变换频谱瀑布。其中图 6(a) 中
频谱。从图 4(b) 可以看出 ˜α-warping 变换的频谱的 出现在 100 ∼ 120 附近的是运动声源，出现在
◦
◦
谱峰频率是一致的，呈现出类似特征频率与距离无 250 ∼ 350 的是强干扰。根据图 6(a) 的目标方位
◦
◦
关的属性。这样对多拍 ˜α-warping 变换频谱进行相 角，对阵列接收信号进行目标方位的波束输出得到
干累加得到高增益的频谱输出。 波束输出信号经warping变换后的频谱如图 6(b)所
图 5 是累加 warping 变换获得的时间增益随快 示，其中假定warping变换的距离为7 km，图中每一
拍数的变化，其中图 5(a) 阵列输出信噪比是 3 dB， 距离处的warping变换频域信号做了归一化处理。
图 5(b) 阵列输出信噪比是 6 dB。对比两图可以看
2500
出单阵元信噪比较低的情况下，累加 warping 变换
得到的时间增益是有损失的，在信噪比较高的情况 2000
下噪声能量较小，多拍 warping 变换得到增益越接 1500
近理论计算值。 ~/s α
1000
3 实验数据分析 500 ଢԩϙ
ᄾࠄϙ
利用 2005 年中国科学院声学研究所在北黄海 0 2 3 4 5 6 7
浅海海域的一次海底水平阵声学测量实验对方法 ᡰሏ/km
~
(a) α ᬤ௑ᫎѬ࣋
ᑟ᧚/dB 1.0
70 7 0.9
2000 0.8
65 6
0.7
1500 5 0.6
௑ᫎ/s 60 ᡰሏ/km 0.5
1000 4 0.4
55
0.3
500 3 0.2
50
0.1
2
0 50 100 150 200 250 300 350 0 20 40 60 80 100
ᝈए/(O) ᮠဋ/Hz
(a) CBF (b) α-warpingԫ૱༙࣋
~
60
1.0
55 100થኄʷጸ៨࢏ᮠဋ
7 0.9 ӭથኄʷጸ៨࢏ᮠဋ
0.8 50 100થኄ̄ጸ៨࢏ᮠဋ
6 0.7 45 ӭથኄ̄ጸ៨࢏ᮠဋ
ᡰሏ/km 5 0.6 ᮠဋ/Hz 40
0.5
35
4 0.4 30
0.3
25
3 0.2
0.1 20
2 15
0 20 40 50 50 100 1 2 3 4 5 6 7 8
ᮠဋ/Hz ᡰሏ/km
(b) warpingԫ૱ᮠ៨ (c) ៨࢏ᮠဋ
图 6 CBF 和阵列输出 warping 变换频谱 图 7 ˜ α 的分布、˜α-warping 变换频谱和谱峰频率
Fig. 6 CBF and warping transform spectrum of Fig. 7 The distribution of ˜α, ˜α-warping transform
array output signal spectrum and spectral peak frequency