Page 92 - 《应用声学》2022年第1期

88 2022 年 1 月

频率为 f 的正向传播的模态 n 兰姆波在均匀板 2.5
中的位移场为
2.0
 
U n (y) [ ( )]
f
u(x, y, t)=   exp i −k x + 2πft ,
n
V n (y) 1.5
(9) ξ/(10 -8 m·W -0.5 ) 1.0
表达式为复数形式，取表达式的实部表示实际位移
值。下标为模态编号，上标表示频率，模态 n 的波数 0.5
由频散关系确定，令 k > 0。模态 n 在薄板上表面
f
n
0
的离面位移可以写成行波的形式： 0 0.2 0.4 0.6 0.8 1.0 1.2
ᮠԒሥ/(MHz·mm)
[ ( f )]
u (x, t) = U n (h) exp i −k x + 2πft . (10)
n
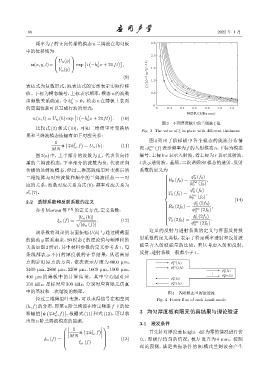
图 3 不同厚度板中的兰姆波 ξ 值
比较式 (3) 和式 (10)，可知二维傅里叶变换结
Fig. 3 The value of ξ in plate with different thickness
果和兰姆波模态振幅有如下对应关系：
图 4 列出了阶梯板中各个模态的能流分布情
1 ( f )
ˆ u ∓k , f = U n (h) . (11) inc (f)表示频率为f 的入射模态n，下标为模态
n
MN 况，ϕ n
图 2(a) 中，上半部分的波数为正，代表负向传 编号，上标 inc 表示入射波，若上标为 r 表示反射波，
播的兰姆波模态，下半部分的波数为负，代表正向 t 表示透射波。基频、二次谐频 S0 模态的透射、反射
传播的兰姆波模态，经过二维离散傅里叶变换后的 系数的定义为
 r
二维矩阵与对应波数和频率的兰姆波模态一一对  ϕ (f 0 )
0
R 0 (f 0 ) = inc ,

应的关系，波数对应关系为式 (8)，频率对应关系为  ϕ 0 (f 0 )



 t
 ϕ (f 0 )
式 (7)。  0 ,
T 0 (f 0 ) =

ϕ (f 0 )
 inc
0 (14)
2.2 透射系数和反射系数的定义 r
 ϕ (2f 0 )
0
R 0 (2f 0 ) = ,

参考Morvan等 [15] 的定义方式，定义系数：  ϕ inc (2f 0 )

0



 t
|V n (h)|  ϕ (2f 0 )
0

. (12) T 0 (2f 0 ) = .

ξ n (f) = √ inc
|ϕ n (f)| ϕ 0 (2f 0 )
该系数将理论的表面振幅 U(h) 与通过横截面 这里的反射与透射系数的定义与界面反射投
射系数的定义类似，表示了特定频率透射和反射波
的能流 φ 联系起来，S0 模态 ξ 的理论值与频厚积的
关系如图 3 所示，其中材料参数的定义参考表 1，每 能量占入射波能量的比值。若只考虑入射和反射，
条线都表示不同的厚度板的计算结果，从远离原 反射、透射系数一般都小于1。
点到靠近原点的方向，依次表示厚度为 4000 µm、 φ ↼f  ↽

inc

inc
3400 µm、2800 µm、2200 µm、1600 µm、1000 µm、 φ ↼f ↽ φ ↼f ↽

t

t
400 µm 的薄板中的计算结果。其中空心圆对应 φ ↼nf  ↽

r
φ ↼f  ↽

r
150 kHz，星标对应 300 kHz，分别对应有限元仿真 φ ↼f ↽

中的基波和二次谐波的频率。 图 4 各阶模态兰姆波能流
经过二维傅里叶变换，可以求得信号在相空间 Fig. 4 Power flux of each Lamb mode
(k, f)的分布，即第n 阶兰姆波在给定频率f 下的位
( ) 3 均匀厚度板有限元仿真结果与理论验证
移幅值 ˆ u ∓k , f ，根据式 (11) 和式 (12)，可以求
f

n
出第n阶兰姆波模态的能流：
3.1 激发条件
 2
1 ( )
f
ˆ u ∓k , f 首先针对厚度差height_dif为零的情况进行仿
n
 MN 
ϕ n (f) =   . (13) 真，即板厚均匀的情况，板厚设置为 4 mm。按照
 ξ n (f) 
理论预测，满足共振条件的 S0 模式兰姆波会产生