Page 93 - 《应用声学》2022年第5期

第 41 卷 第 5 期 潘宇雄等： 双锥型五模材料低频声波调控及参数设计 769

布基本相同。在五模材料以外的区域, 平面波特征 由于五模材料难以被压缩，在传输波时发生的
得到了很好的保持，故这种五模材料和水在声学上 形变远小于自身结构尺寸，根据连续介质力学的质
的传播特性相似，具有较好的水声学匹配特性。五 量守恒定律，可认为在这种小应变下的前后密度保
模材料这一声波调控特性，使其对于水中 “声隐身” 持布标，即等效质量密度 ρ B 和 ρ G 可看作静态质量
领域具有潜在前景。 密度ρ 0 ，此时五模品质因数与相速度的关系为
freq(5)=250 Hz ᛫᭧὘঴ܦԍڤ (Pa) 1.0
( ) 2
0.8 FOM = B/G = C B /C G . (4)
0.6
0.4
0.2 通过计算能带图中压缩波和剪切波对应的能带
0 曲线斜率，可以进一步求得 C B 和 C G 的值 [11−12] 。
-0.2
-0.4 从 图 3 中 压 缩 波 和 剪 切 波 的 能 带 曲 线 斜 率 求
-0.6
-0.8 得 六 边 形 排 列 五 模 材 料 的 五 模 品 质 因 数 FOM
-1.0
≈ 1910.1 > 10 ，故这种五模材料结构有较好
3
(a) ෥ద̋വెந
的五模特征，可对声波传播进行调控。
freq(5)=250 Hz ᛫᭧὘঴ܦԍڤ (Pa) 1.0
0.8
0.6 1.4 正方形排列构型
0.4
0.2 由于六边形排列双锥五模材料的声子带隙带
0
-0.2 宽较小，为得到更宽的带隙，按如图9(a)所示构造正
-0.4 方形排列双锥五模材料。胞元的晶格常数 a 保持不
-0.6
-0.8 变为 16 mm，其他几何参数包括双锥宽 D = 3 mm，
-1.0
(b) ద̋വెந 节点半径 r = 0.3 mm。同样选择 TC4 钛合金和硫
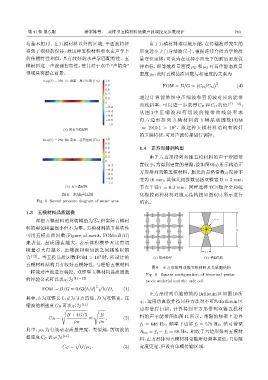
图 8 水域声压图 化橡胶两种材料对胞元结构按如图 6(b) 所示进行
Fig. 8 Sound pressure diagram of water area 填充。

1.3 五模材料品质因数
理想五模材料的剪切模量为零，但实际五模材 r
料的剪切模量很小但不为零。五模材料的五模特性 a

可用五模品质因数 (Figure of merit，FOM=B/G)
来表征，品质因素越大，表示体积模量 B 比剪切
模量 G 大得越多，压缩波和剪切波之间越难以耦
D
3
合 [12] 。当五模品质因数 FOM > 10 时，所设计的 (a) ଆѵ౞ی (b) ӭᑊፇ౞
五模材料结构具有较好五模特性，与理想五模材料
图 9 正方形排列双锥五模材料及其单胞结构
一样能对声波进行调控。双锥型五模材料品质因数
Fig. 9 Square configuration of biconical penta-
的经验公式可以表示为 [11−12] mode material and the unit cell
( ) √
2
FOM = B/G ≈ 0.63 h/d h/D, (1)
正方形排列单胞的简约 Brillouin 区如图 10 所
其中，h 为双锥长 L，d 为节点直径，D 为双锥宽。压
示，运用仿真软件按同样方法对不可约 Brillouin 区
缩波的相速度C B 可表示为 [11]
边界进行扫描，计算得到正方形排列双锥五模材
√ √
B + 4G/3 B 料的声子能带图如图 11 所示。带隙的频率上边界
C B = ≈ , (2)
ρ B ρ B
f t = 646 Hz，频率下边界 f l = 578 Hz，绝对带宽
其中，ρ B 为有效动态质量密度。类似地，剪切波的 A bw = f t − f l = 68 Hz。相较于六边形排列五模材
相速度C G 表示为 [11] 料，正方形排列五模材料带隙所处频率更低，且带隙
√
C G = G/ρ G . (3) 宽度更宽，但没有单模传输区域。