Page 48 - 《应用声学》2023年第3期

486 2023 年 5 月

这里的波束方向图案 Bp(sin θ| sin ϑ) 是当远场 ˆ s (k+1) (x)
点源的方向正弦值为 sin ϑ 时，该线性系统在输出  
ˆ s (0) (x) ∑ h(z|x)B(z)
方向正弦值为 sin θ 时的响应 (即波束能量)。已知 = ∑  ∑  . (15)
′
′
h(z|x) h(z|x )ˆs (k) (x )
B CBF 和 Bp 反求声源分布 S(sin ϑ)，这样就得到关 z∈Z x ∈X
′
z∈Z
于声源目标的方位估计。注意到 Bp(sin θ| sin ϑ) 的
在很多实际的应用场景中，对于所有的x 而言，
移位不变性，即Bp(sin θ| sin ϑ) = Bp(sin θ − sin ϑ)， ∑
公式 (15) 的分母 h(z|x) 恒为 1，因为 h(z|x)
那么声源分布 S(sin ϑ) 的估计问题就变成了一个典 z∈Z
通常被看作为一个积分和为 1 概率密度函数。但在
型的反褶积问题。利用上述序列 [12] ，反褶积作用在 ∑
本文的讨论中， h(z|x) 是一个关于变量 x 的
波束能量域 (非负的)，且是适定的。在水声环境中， z∈Z
∑
当海底环境参数随方位变化或接收阵列为任意形 函数，分母中含有 h(z|x) 相当于进行了归一
z∈Z
状时Bp(sin θ| sin ϑ) ̸= Bp(sin θ − sin ϑ)，即积分： 化。此外，初始估计值 ˆs (0) (x) 可以设置为任意一个
∫ 1 非负的概率密度函数，本文选取 ˆs (0) (x) = 1/M，M
M(sin θ) = Bp(sin θ| sin ϑ)d sin ϑ (10)
−1 代表集合X中元素的个数。
是关于变量 sin θ 的函数，不是一个定值，需要对其
进行归一化处理。
2 仿真分析
类似于公式 (9)，可以将公式 (8b) 中声源的深
度分布 (系统输入) 和 B(r s , z)(系统输出) 间的关系 将基于 SWellEx-96 实验 [22] 中的 Event S5，用
表示为第一类弗雷德霍姆积分方程的形式： 仿真和实验数据对本文提出的方法进行验证。实
∫
∞
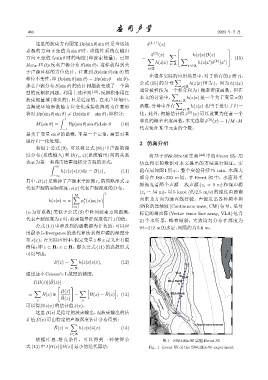
h(z|x)s(x)dx = B(z), (11) 验布局如图 1 所示，整个实验持续 75 min，水深大
−∞ 部分在 180∼220 m 间。在 Event S5 中，水面科考
其中，B(z)是略掉了声源水平距离r s 的简略形式，x
船拖曳着两个声源 —浅声源 (z s = 9 m) 和深声源
代表声源的实际深度，s(x)代表声源深度的分布，
(z s = 54 m)，以 5 knot (约 2.5 m/s) 的速度由西南
2
M
∑
∗ 向东北方向匀速直线行驶。声源发出各种频率和
i
h(z|x) = α φ (z)φ i (x)
SNR的连续波 (Continuous wave, CW) 信号。星号
i=1
(α 为常系数) 类似于公式 (9) 中阵列波束方向图案， 标记的垂直阵 (Vector senor line array, VLA) 包含
代表声源深度为x时，波束能量在深度位置z 的值。 21 个水听器，略有倾斜，大致均匀分布在深度为
公式 (11) 中涉及到的函数都为非负的，可以应 94∼212 m的水层，间隔约为5.6 m。
用最小 I-divergence 的迭代算法求得声源的深度分
布s(x)。在实际应用中，假定变量 z 和x定义在有限
维集，即 z ⊂ R，x ⊂ R。那么公式 (11) 的离散形式
可以写成：
∑
B(z) = h(z|x)s(x), (12)
x∈X
通过最小Csiszar’s I-散度的测度：
ˆ
I[B(z)||B(z)]
[ ]
∑ B(z) ∑ [ ]
ˆ
= B(z) ln − B(z) − B(z) , (13)
ˆ
B(z)
z z
可以得到s(x)的估计值 ˆs(x)。
这里B(z)是给定的波束输出，而波束输出的估
ˆ
计值B(z)可由特定的声源深度估计分布得到：
∑
ˆ
B(z) = h(z|x)ˆs(x). (14)
x⊂X
依据库恩 -塔克条件，可以得到一种使得公 图 1 SWellEx-96 实验 Event S5
ˆ
式 (13)中I[B(z)||B(z)]最小的迭代算法： Fig. 1 Event S5 of the SWellEx-96 experiment