Page 51 - 《应用声学》2023年第3期

第 42 卷 第 3 期 袁笑等： 基于最小 Csiszár’s I-散度的高精度深度定位方法 489

锐峰值，较为准确地实现了相邻深度非相干声源的 为 −5 dB，信干比为 −7 dB，深度分别为 50 m 和
分辨。 150 m，水平距离均为 5000 m，取前 20 号简正波，
深度定位结果如图 8 所示。由于 SNR 较低，对应于
0
声源信号和噪声的特征值相差不大且都小于强干
MCID
CB 扰的特征值，在当前仿真条件下，对基于模式幅度
-5 MV
MUSIC 向量 A (归一化后) 得到的协方差矩阵进行特征值
ฉౌᑟ᧚/dB -10 分解，得到从大到小排列后的前 5 号特征值依次为
0.4918、0.0953、0.0777、0.0544、0.0410；可以发现，此

-15 时声源信号对应的特征值 0.0953 和后面噪声的特
征值难以区分，在实际处理中，若不已知声源数目
D，易将声源信号等同于噪声。结合图8(a)和图 8(b)
-20
50 100 150
可得，若未知声源数目 D，错取 D = 1，MUSIC方法
ງए/m
只能辨别出深度在 50 m 处的强干扰；而 MCID 法、
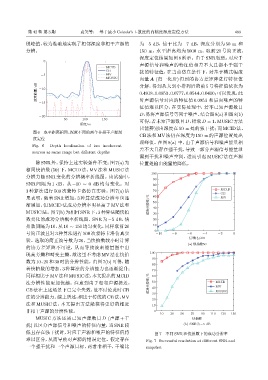
图 6 水平距离相同、深度不同的两个非相干声源深
CB 法和 MV 法仍在深度为 150 m 的声源位置处出
度定位
现峰值。在图 8(a) 中，由于声源信号和噪声能量相
Fig. 6 Depth localization of two incoherent
差不大且存在强干扰，导致一部分声源信号能量泄
sources at same range but different depths
漏到干扰和噪声空间，进而引起 MUSIC 法在声源
除 SNR 外，保持上述实验条件不变；图 7(a) 为 位置处输出能量的降低。
相同快拍数 (50) 下，MCID 法、MV 法和 MUSIC 法
100
分辨力随 SNR 变化的分辨概率折线图。该试验中，
90
SNR 间隔为 1 dB，从 −10 ∼ 0 dB 均匀变化。对 80
3 种算法进行 500 次蒙特卡洛仿真实验。图 7(a) 结 70 MCID
CB
果表明，随着 SNR 增加，3 种算法成功分辨率也逐 60 MV
渐增加，但 MCID 法成功分辨率明显高于 MV 法和 ੇҪѬᣲဋ/% 50
40
MUSIC法。图7(b)为相同SNR下，3 种算法随快拍 30
数变化的成功分辨概率折线图。SNR 为 −5 dB，快 20
拍数间隔为 10，从 10 ∼ 150 均匀变化，同样取前 20 10
0
号简正波且对 3 种算法进行 500 次蒙特卡洛仿真实 -10 -8 -6 -4 -2 0
η٪උ/dB
验。选取的简正波号数为 20，当快拍数较小时计算
(a) ঌથ஝50
的协方差矩阵不可逆，从而导致波束能量图中出
现高旁瓣和畸变主瓣，故这里不考虑 MV 法在快拍 100
90
数为 10、20 和 30 时的分辨性能。由图 7(b) 可得，随
80
着快拍数的增加，3 种算法的分辨能力也逐渐提升； 70
同样相比于MV法和MUSIC法，本文提出的MCID 60
法分辨性能更加优越。注意到由于相邻声源接近， ੇҪѬᣲဋ/% 50 MCID
CB 法在上述场景下已完全失效，故不讨论此时CB 40 MV
MUSIC
30
法的分辨能力。综上所述，相比于传统的CB法、MV
20
法和 MUSIC 法，本文提出方法能获得更好的相近 10
非相干声源的分辨性能。 0
10 30 50 70 90 110 130 150
MUSIC 方法还需已知声源数目 D (声源 + 干 ঌથ஝
扰) 以区分声源信号和噪声的特征向量，当 SNR 较 (b) SNR˞-5 dB
低且存在强干扰时，对应于声源和噪声的特征值将 图 7 不同 SNR 和快拍数下的成功分辨率
难以区分，从而导致对声源的错误定位。假定存在 Fig. 7 Successful resolution at different SNR and
一个强干扰和一个声源目标，两者非相干，干噪比 snapshot