Page 50 - 《应用声学》2023年第3期
P. 50
488 2023 年 5 月
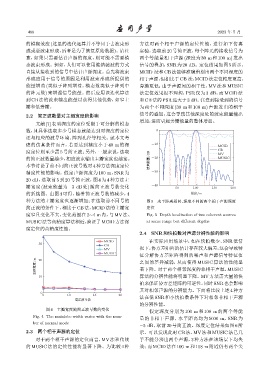
的模糊效应 (这里的迭代运算并不等同于去波束形 方法对两个相干声源的定位性能,进行如下仿真
成或逆波束形成,后者是为了恢复原始数据)。请注 实验,选取前 20 号简正波,每个阵元的接收信号为
意,如果只需要估计声源的深度,则可能不需要模 两个等能量相干声源 (深度为 30 m 和 100 m) 发出
态波束形成。例如,人们可以使用维纳滤波的方式 信号的叠加,SNR 为 20 dB。定位结果如图 5 所示,
直接从接收到的信号中估计声源深度。首先将波束 MCID 法和CB 法能够准确辨别出两个不同深度的
形成应用于信号的原因是利用波束形成所提供的 相干声源,但相比于CB 法,MCID法定位精度更高,
能量增益 (类似于阵列增益,模态数类似于阵列中 旁瓣更低;由于声源间的相干性,MV 法和 MUSIC
的阵元数) 来增强信号能量。然后应用该迭代算法 法定位效果很不理想,PSR 仅为 3 dB,而 MCID 法
到 CB 法的波束输出能量以获得其他优势,如窄主 和CB法的PSR远大于3 dB。注意到接受到的信号
瓣和低旁瓣。 为两个不同深度 (30 m 和 100 m) 声源发出的相干
2.2 简正波数量对主瓣宽度的影响 信号的叠加,这会导致其他深度处的波束能量输出
增加,进而引起旁瓣能量的整体增加。
文献 [7] 表明深度的定位受限于可分解的模态
数,且具体选取多少号模态就能达到对深度的定位 0
还与相应的波导环境、阵列孔径等相关。就本文考
虑的仿真条件而言,若要达到精度小于 40 m 的深 -10 MCID
度定位则至少需 5 号简正波;另外,一般来说,选取 CB
MV
的简正波数量越少,相应波束输出主瓣宽度也越宽。 ฉౌᑟ᧚/dB -20 MUSIC
本节讨论了前不同简正波号数对 4种方法深度定位
精度性能的影响。假定声源深度为 100 m,SNR 为 -30
20 dB,选取前 5 到 20 号简正波,图 4 为 4 种方法主
瓣宽度 (波束能量为 −3 dB 处) 随简正波号数变化 -40 50 100 150 200
的折线图。由图 4 可得,随着简正波号数的减少,4 ງए/m
种方法的主瓣宽度也逐渐增加;在选取前不同号的 图 5 水平距离相同、深度不同的两个相干声源深度
简正波的条件下,相比于 CB 法,MCID 法的主瓣宽 定位
度窄且变化不大,变化范围在 2∼4 m 内,与 MV 法、 Fig. 5 Depth localization of two coherent sources
MUSIC法等高精度算法相近,验证了MCID方法深 at same range but different depths
度定位的高精度性能。
2.4 SNR和快拍数对声源分辨性能的影响
MCID 在实际应用场景中,如在快拍数少、SNR 低情
30
CB
MV 况下,协方差矩阵的估计存在较大偏差,这会导致特
MUSIC
征分解协方差矩阵得到的噪声和声源信号特征值
˟ၥࠕए/m 之间的差异减弱,从而使得 MUSIC 算法的性能显
20
著下降。对于两个相邻深度的非相干声源,MUSIC
10 算法的分辨性能将明显下降。MV 方法需大量的快
拍来保证协方差矩阵的可逆性,同时 SNR也会影响
其对相邻声源的分辨能力。下面将比较上述 4 种方
0
5 10 15 20 法在低 SNR 和小快拍数条件下对相邻非相干声源
እฉՂ
的分辨性能。
图 4 主瓣宽度随简正波号数的变化
假定深度分别为 100 m 和 108 m 的两个等能
Fig. 4 The mainlobe width varies with the num-
量的非相干声源,水平距离均为 5000 m,SNR 为
ber of normal mode
−5 dB,取前 20 号简正波。深度定位结果如图 6 所
2.3 两个相干声源的定位 示。可以发现此时 CB 法、MV 法和 MUSIC 法已几
对于两个相干声源的定位而言,MV 法和传统 乎不能分辨出两个声源,3 种方法在该场景下均失
的 MUSIC 法的定位性能将显著下降。为比较 4 种 效;而 MCID 法在 100 m 和 108 m 附近仍有两个尖