Page 52 - 《应用声学》2023年第3期

490 2023 年 5 月

0 8
MCID L/
CB L/
-5 MUSIC(D=2) 6 L/
L/
L/
ฉౌᑟ᧚/dB -10 ˟ၥࠕए/m 4

-15
2

-20
50 100 150 0
500 1000 1500 2000 2500 3000
ງए/m
ᤖ̽൓஝
(a) MCIDnjCB֗MUSIC(D=2)
(a) SNR˞20 dB
0 8
MV SNR=20
MUSIC(D=1) SNR=15
-5 6 SNR=10
SNR=5
ฉౌᑟ᧚/dB -10 ˟ၥࠕए/m 4
SNR=0

-15 2

-20
50 100 150 0
500 1000 1500 2000 2500 3000
ງए/m ᤖ̽൓஝
(b) MV֗MUSIC(D=1) (b) እ൤ฉՂ஝20
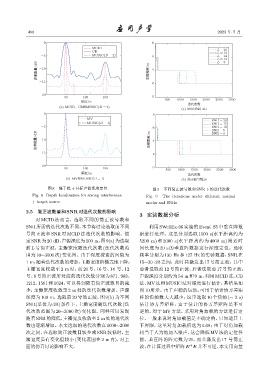
图 8 强干扰 + 目标声源深度定位 图 9 不同简正波号数和 SNR 下的迭代次数
Fig. 8 Depth localization for strong interference Fig. 9 The iterations under different normal
+ target source modes and SNRs

2.5 简正波数量和SNR对迭代次数的影响
3 实验数据分析
对 MCID 法而言，选取不同的简正波号数和
SNR所需的迭代次数不同，本节将讨论选取前不同 利用 SWellEx-96 实验的 Event S5 中垂直阵数
号简正波和 SNR 对 MCID 法迭代次数的影响。假 据进行处理。这里分别选取 1500 s(水平距离约为
定SNR为20 dB，声源深度为100 m，图9(a)为选取 5200 m) 和 2000 s(水平距离约为 4000 m) 附近时
前 L 号简正波，主瓣宽度随迭代次数 (迭代次数范 间长度为 20 s 的垂直阵数据进行深度定位。选取
围为 10∼3000 次) 变化图。由于深度搜索的间隔为 频率分别为 130 Hz 和 127 Hz 的实验数据，SNR 在
1 m，随着迭代次数的增加，主瓣宽度阶梯式地下降； 15∼20 dB 之间，此时共激发出 17 号简正波，其中
主瓣宽度收敛至 2 m 时，前 20 号、16 号、14 号、12 前者选取前 12 号简正波，后者选取前 17 号简正波；
号、8 号简正波所对应的迭代次数分别为 871、963、 声源深度分别约为 54 m 和9 m，利用 MCID法、CB
1212、1561 和 1624，可以得到随着简正波数目的减 法、MV 法和 MUSIC 法对深度进行估计，其结果如
少，主瓣宽度收敛至 2 m 处的迭代次数增加。声源 图 10 所示。由于声源的运动，可用于估计协方差矩
深度为 100 m，选取前 20 号简正波，图 9(b) 为不同 阵的快拍数大大减少；这里选取 10 个快拍 (∼ 2 s)
SNR(单位为 dB) 条件下，主瓣宽度随迭代次数 (迭 估计协方差矩阵，由于估计的协方差矩阵是不可
代次数范围为 20∼3000 次) 变化图。同样可以发现 逆的，对于 MV 方法，采用对角加载的方法进行定
随着 SNR的降低，主瓣宽度收敛至 2 m 处的迭代次 位，一般来说对角加载值是不确定的，只知道其上
数也逐渐增加。本文选取的迭代次数在 1000∼2000 下界限，这里对角加载值选为 0.08；由于对角加载
次之间，在选取简正波数目较少或 SNR 较低时，主 相当于人为地加入噪声，这会降低 MV 法的定位性
瓣宽度虽有变化但较小 (变化范围在 2 m 内)，对上 能。垂直阵的阵元数为 21，而共激发出 17 号简正
面的仿真讨论影响不大。 波，在计算过程中矩阵 E E 并不可逆，本文用向量
+