Page 119 - 《应用声学》2023年第6期

第 42 卷 第 6 期 杜阔等： 非轴对称五模超材料低频声波调控分析 1229

向与波矢平行，图 3(f) 中质点的振动方向与波矢垂 示体积模量 B 相对剪切模量 G 越大，纵波和横波
直，同样的可以得到 C、D 处波矢方向与质点振动方 之间越难以耦合。当五模品质因数 FOM > 1000
向的关系，即A、C 点对应纵波模式，B、D 点对应横 时，即所设计的五模材料结构具有较好五模特性，
波模式。这意味着在灰色区域只允许纵波传播而横 与理想五模材料一样能对声波进行调控，品质因
波被抑制，表征了五模超材料在这一频段区域的流 数可由纵波和横波对应能带曲线斜率比值的平方
体特性。 求得 [21] 。图 3(b) 中掺杂母胞的第一带隙频率上界
此外，为了体现五模超材料在禁带频域范围内 f T 1 = 781 Hz，频率下界 f l1 = 716 Hz，绝对带宽
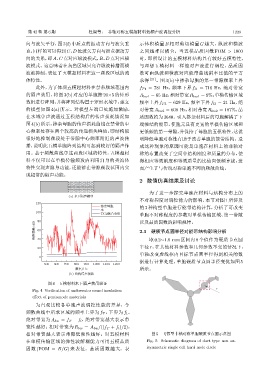
的隔声效用，将图 3(b) 对应的单胞按 20×5 的矩形 A bw1 = 65 Hz，相对带宽R bw1 = 9%；单模传输区域
数组进行阵列，并将阵列结构置于矩形水域中，建立 频率上界 f T 2 = 629 Hz，频率下界 f l2 = 21 Hz，绝
的模型如图 4(a) 所示。对模型左端口处施加激励， 对带宽 A bw2 = 608 Hz，相对带宽 R bw2 = 187%，品
在水域中声波通过五模结构后的传声损耗情况如 质因数约为3640。引入掺杂材料后的母胞解耦了下
图4(b) 所示，掺杂母胞的传声损耗曲线在禁带的中 端缠结的能带，使胞元具有更宽的单模传输区域和
心频率处存在两个较高的传递损失峰值，即结构能 更低频的第一带隙，并保持了母胞的五模特性，这说
很好地抑制频段处于带隙中心频率附近的声波传 明降低单胞对称性有助于改善单胞的能带结构。造
播，说明此五模单胞阵列结构可起到较好的隔声作 成这种现象的原因可能是单胞在材料上的非轴对
用。基于频散曲线中这两段区域的特性，五模超材 称的布置改变了空间中结构刚度和质量的分布，使
料不仅可以在单模传输频段内利用自身的类流体 得相应等效刚度和等效质量的比值向低频靠拢，进
特性实现声隐身功能，还能够在带隙频段范围内实 而产生了与传统对称单胞不同的频散曲线。
现超常的隔声功能。
2 数值仿真结果及讨论

为了进一步探究单胞在材料与结构分布上的
(a) ඵʾᬦܦവی
不对称程度对调控能力的影响，本节对图 1 所涉及
120
ଙాඇᑊ 的 3 种构型单胞进行能带结构计算，分析了可改变
ඵ
100 TC4᧻Ռ᧛ڱ 单胞不对称程度的参数对单模传输区域、第一带隙
80 以及品质因数的影响规律。
͜ܦ૯Ᏺ/dB 60 2.1 取 0.2∼1.6 mm 区间内 8 个值作为硬质节点圆
硬质节点圆半径对能带结构影响分析

40
20 半径 r，在其他材料参数和几何参数不变的情况下，
单独改变虚线框内目标节点圆半径得到相关的数
0
据进行计算处理，单胞硬质节点圆半径变化如图 5
500 600 700 800 900 1000 1100 1200
ᮠဋ/Hz 所示。
(b) ፇ౞͜ܦ૯Ᏺ

图 4 五模材料水下隔声效用验证
Fig. 4 Verification of underwater sound insulation r
effect of pentamode materials
为直观比较各单胞声波调控性能的差异，令
频散曲线中所求区域的频率上界为 f T ，下界为 f l 。
绝对带宽为 A bw = f T − f l ，绝对带宽越大表示带
宽性越好；相对带宽为 R bw = A bw /((f T + f l )/2)，
相对带宽越大表示带隙低频性越好。对五模材料 图 5 飞镖型非轴对称单胞硬质节点圆示意图
在单模传输区域的弹性波解耦能力可用五模品质 Fig. 5 Schematic diagram of dart type non ax-
因数 (FOM = B/G) 来表征，品质因数越大，表 isymmetric single cell hard node circle