Page 111 - 《应用声学》2024年第1期

第 43 卷 第 1 期 贺佐潦霜等： 矩形单元声场波函数构造及其应用 107

20×20 个测点。重建面在简支板正上方 0.01 m 处， Лৌ᧔ನ᭧
尺寸与简支板大小相同，均匀分布 40×40 个重建测 0.03
点。虚源面尺寸与简支板大小相同，均匀划分为 0.02
20×20 个正方形单元，单元长度为 0.025 m，并用面 ᧘थ᭧
0.01
积相同的圆形域代替正方形单元，在每一个单元中 z/m
心布置一个等效源点，模型示意如图 5 所示。将虚 0 እஃ౜
源面分别置于重建面下方0.5倍、1倍、2倍单元长度 -0.01
位置，并在仿真中对全息面测量声压添加信噪比为
-0.02
30 dB 的高斯白噪声，然后对比圆形域内推波函数 0.5 ᘿલູू᭧ 0.5
与ESM重建声场的相对误差。 y/m 0 0 x/m

表 3 仿真参数
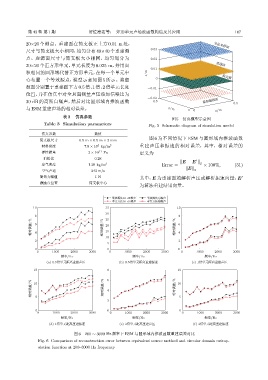
图 5 仿真模型示意图
Table 3 Simulation parameters Fig. 5 Schematic diagram of simulation model
仿真参数 数值
图 6 为不同情况下 ESM 与圆形域内推波函数
简支板尺寸 0.5 m × 0.5 m × 2 mm
材料密度 7.8 × 10 kg/m 3 重建声压和振速的相对误差，其中，相对误差的
3
弹性模量 2 × 10 11 Pa 定义为
泊松比 0.28
′
∥E − E ∥
空气密度 1.29 kg/m 3 Error = 2 × 100%, (31)
∥E∥
空气声速 343 m/s 2
简谐力幅值 1 N ′
其中，E 为重建面的解析声压或解析振速向量，E
激励点位置 简支板中心
为算法重建结果向量。
኎஍ູข30 dB٪ܦ ኎஍ູข௄٪ܦ
వ஡வข30 dB٪ܦ వ஡வข௄٪ܦ
10 35 10
30
8 25 8
ᄱࠫឨࣀ/% 6 ᄱࠫឨࣀ/% 20 ᄱࠫឨࣀ/% 6

15
4
10 4
2 2
5
0 0 0
0 1000 2000 3000 0 1000 2000 3000 0 1000 2000 3000
ᮠဋ/Hz ᮠဋ/Hz ᮠဋ/Hz
(a) 0.5φӭЋᡰሏ᧘थܦԍ (b) 0.5φӭЋᡰሏ᧘थ૝ᤴ (c) 1φӭЋᡰሏ᧘थܦԍ
15 8 15

ᄱࠫឨࣀ/% 10 ᄱࠫឨࣀ/% 6 4 ᄱࠫឨࣀ/% 10

5
2 5

0 0 0
0 1000 2000 3000 0 1000 2000 3000 0 1000 2000 3000
ᮠဋ/Hz ᮠဋ/Hz ᮠဋ/Hz
(d) 1φӭЋᡰሏ᧘थ૝ᤴ (e) 2φӭЋᡰሏ᧘थܦԍ (f) 2φӭЋᡰሏ᧘थ૝ᤴ

图 6 200 ∼ 3000 Hz 频率下 ESM 与圆形域内推波函数重建误差对比
Fig. 6 Comparison of reconstruction error between equivalent source method and circular domain extrap-
olation function at 200–3000 Hz frequency