Page 112 - 《应用声学》2024年第1期

108 2024 年 1 月

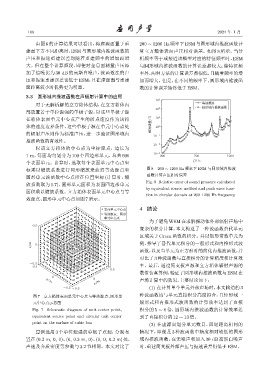
由图 6 的计算结果可以看出，将虚源面置于重 200 ∼ 1200 Hz频率下ESM与圆形域内推波函数计
建面下方不同距离时，ESM与圆形域内推波函数的 算立方箱体表面声压相对误差。如图 8 所示，当分
声压和振速重建误差均随着重建频率的增加而增 析频率等于或接近该模型对应的特征频率时，ESM
大。但在整个计算频段，即便对全息面测量声压添 与圆形域内推波函数的计算误差都较大；除特征频
加了信噪比为 30 dB 的高斯白噪声，波函数法的声 率外，两种方法的计算误差都很低，且随着频率的增
压和振速重建误差也低于ESM，且在虚源面与重建 加而增大。但是，在不同的频率下，圆形域内推波函
面距离较小时优势更为明显。 数的计算误差始终低于ESM。
3.3 圆形域内推波函数在声辐射计算中的应用
10 3
对于无解析解的立方箱体结构，在立方箱体内 ኎஍ູข
10 2 ړॎ۫Я଎ฉѦ஝
部放置若干单位源强的单极子源，以这些单极子源
在箱体表面单元中心点产生的质点速度作为该箱 10 1
体的速度边界条件，这些单极子源在单元中心点处 ᄱࠫឨࣀ/% 10 0
的辐射声压则作为标准声压，进一步验证圆形域内
10 -1
推波函数的有效性。
10 -2
以该立方箱体的中心点为坐标原点，边长为
10 -3
1 m，每面均匀划分为 100 个四边形单元，总共 600 200 700 1200
个表面单元。计算时，选取每个表面单元中心点坐 f/Hz
标乘以缩放系数进行同形缩放来获得等效源点和 图 8 200 ∼ 1200 Hz 频率下 ESM 与圆形域内推波
圆形单元波函数中心点所在位置坐标 (计算时，缩 函数计算声压相对误差
Fig. 8 Relative error of sound pressure calculated
放系数取为 0.7)，圆形单元面积为表面四边形单元
by equivalent source method and push wave func-
面积乘以缩放系数。立方箱体表面单元中心点与等
tion in circular domain at 200–1200 Hz frequency
效源点、圆形单元中心点如图7所示。

᛫᭧ӭЋ˗ॷག 4 结论
኎஍ູགnjړॎ
ӭЋ˗ॷག
为了避免WSM在求解振动体外部辐射声场中
0.5
复杂的积分计算，本文构造了一种波函数替代单元
区域关于 Green 函数的积分。并以矩形常数单元为
z/m 0 例，推导了替代单元积分的一般形式和内推形式波
函数，以及当单元为正方形时的简化内推波函数，并
对比了 3种波函数与直接积分的计算精度和计算效
-0.5
0.5 率。最后，通过简支板声源和立方箱体辐射声源的
0.5
数值仿真算例，验证了圆形域内推波函数与ESM在
0
0 声场计算中的效果，主要结论如下：
x/m
y/m
(1) 在计算单个单元外部声场时，本文构造的 3
-0.5 -0.5
图 7 立方箱体表面单元中心点与等效源点、圆形单 种波函数均与单元直接积分高度拟合，且矩形域一
元中心点示意图 般形式和内推形式波函数的计算效率达到了直接
Fig. 7 Schematic diagram of unit center point, 积分的 5 ∼ 6 倍，圆形域内推波函数的计算效率达
equivalent source point and circular unit center 到了直接积分的12 ∼ 13倍。
point on the surface of cubic box
(2) 在虚源面划分单元数目、回退距离相同的
算例选用 3 个单位源强的单极子点源，分别布 情况下，即便是 3 种波函数中精度相对较低的圆形
置在 (0.3 m, 0, 0)、(0, 0.3 m, 0)、(0, 0, 0.3 m) 处， 域内推波函数，在无噪声和加入 30 dB 高斯白噪声
声速及介质密度等参数与 3.2 节相同。本文对比了 时，重建简支板外部声压与振速误差仍低于ESM。