Page 232 - 《应用声学》2025年第3期

766 2025 年 5 月

如图5所示。 在群速度曲线图 5(b)，对于不同传播模态，各
从图 5 中可看出，充黏液孔隙介质圆柱壳中 模态的频散程度也不尽相同，当频率有很小的变化
超声导波纵向模态具有以下特点。在相速度曲线 时，群速度都会发生很大的变化。除 α 和 L(0, 1) 模
图 5(a)，在频带 0 ∼ 0.45 MHz 内共有 13 个纵向 态，每个传播模态群速度曲线的变化趋势，几乎都
模态：α 模态和 L(0, 1 ∼ 12) 模态。在低频段 0 ∼ 是随着频率的增加而达到最大值，然后逐渐减小再
0.03 MHz，模型中只存在 2 个纵向模态：α 模态和 增加，最终趋近于自由状态下黏液的纵波波速，此
L(0, 1) 模态。α 模态是只存在于充液圆柱中的纵向 时群速度和相速度相等，即为非频散状态。在频段
模态，Aristégui 等 [36−37] 通过实验测定验证了该模 0∼0.03 MHz 时，L(0, 1) 模态的频散较小；当频率大
态的存在，并认为其在液体中的径向位移和轴向 于0.05 MHz 时，L(0, 1)模态几乎是非频散的，因此，
位移随着距圆柱内壁的距离呈指数下降，能量主 L(0, 1) 是可选择的适于测量圆柱壳孔隙含量的模
要在圆柱内部的液体中传播，该模态的运动类似于 态。而在一定的频率区域，L(0,2∼12)等高阶模态均
Scholte 波，这种模态不适用于激励，不满足检测的 出现群速度的最大值，并且在最大值附近，群速度曲
需要。超声导波的纵向模态中仅α 和L(0, 1)模态不 线趋于平坦，模态的频散很小，满足检测的需求，也
存在截止频率，α 模态的相速度先减小后增加，高频 是可选择的潜在检测模态。
趋近于1.389 km/s，略小于黏液的纵波波速，其他模
2.4 孔隙度对导波频散的影响
态的相速度随着频率的增加逐渐减小，最终趋近于
为了进一步分析充黏液孔隙介质圆柱壳中导
自由状态下黏液的纵波波速1.530 km/s [38] 。
波频散特性受孔隙度的影响，明确孔隙度与导波频
5.0
散受影响的关键频段部分。在孔隙介质黏滞系数
为 10 −3 kg·m ·s 条件下，取孔隙度为 0.05、0.10 和
1
1
L(0,12)
4.0
0.20，其他参数不变，对充黏液孔隙介质圆柱壳中的
ᄱᤴए/(km⋅s -1 ) 3.0 L(0,2) L(0,3) 度充黏液孔隙介质圆柱壳中超声导波纵向模态相
前 6 阶模态频散的情况进行研究。图 6 为不同孔隙
速度频散曲线。
2.0
L(0,1)
5.0
1.0 4.5 ߘᬩए β=0.05
ߘᬩए β=0.10
4.0
ߘᬩए β=0.20
0 3.5
0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 3.0
ᮠဋ/MHz L(0,5)
(a) ᄱᤴए ᄱᤴए/(km⋅s -1 ) 2.5
2.0
3.5 1.5
L(0,2) L(0,3) L(0,1) 3.0
3.0 1.0 2.5
α 2.0 0 0.05 0.10
L(0,1)
0.5
Ꮖᤴए/(km⋅s -1 ) 2.0 L(0,12) 0 0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45
1.5
2.5
ᮠဋ/MHz
1.5
相速度频散曲线
1.0 图 6 不同孔隙度下充黏液孔隙圆柱中纵向模态的
Fig. 6 Phase velocity dispersion curves of longi-
0.5 α
tudinal modes in the porous cylinder filled with
0
0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 viscous liquid
ᮠဋ/MHz
(b) Ꮖᤴए 从图 6 中可以看出，孔隙度对 α 模态影响不明
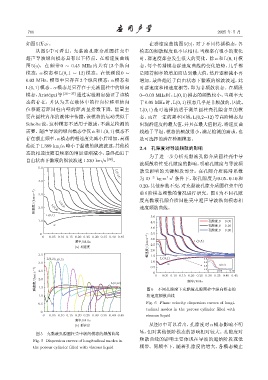
图 5 充黏液孔隙圆柱壳中纵向模态的频散曲线 显，但对其他低阶模态的影响相对较大。孔隙度对
Fig. 5 Dispersion curves of longitudinal modes in 频散曲线的影响主要体现在导波的起始阶段或低
the porous cylinder filled with viscous liquid 频带。同频率下，随着孔隙度的增大，各模态截止