Page 231 - 《应用声学》2025年第3期

第 44 卷 第 3 期 苏娜娜等： 孔隙度检测长骨骨质疏松的超声导波传播特性 765

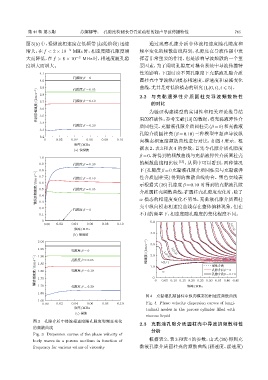
图3(b) 中，慢纵波相速度在低频带 (起始阶段) 迅速 通过观察孔隙介质中体波相速度随孔隙度和
增大，在 f < 2 × 10 −3 MHz 时，相速度随孔隙度增 频率变化的频散曲线得到，孔隙度在导波传播中发
大而降低，在 f > 6 × 10 −3 MHz 时，相速度随孔隙 挥着非常重要的作用，也是影响导波频散的一个重
度增大而增大。 要因素，为了阐明孔隙度对耦合系统中导波传播特
4.1 性的影响，下面讨论不同孔隙度下充黏液孔隙介质
ߘᬩए β=0
4.0 圆柱壳中导波纵向模态相速度、群速度和衰减变化
3.9 ߘᬩए β=0.05 曲线，尤其是对低阶模态的研究(L(0, i), i 6 5)。
ঌጫฉᄱᤴए/(km⋅s -1 ) 3.7 ߘᬩए β=0.10 2.2 为验证构建模型的实用性和相关理论推导结
3.8
与 充 黏 液 弹 性 介 质 圆 柱 壳 导 波 频 散 特 性
的对比
3.6
3.5
3.4 果的准确性，参考文献[13] 的数据，将充黏液弹性介
质圆柱壳、充黏液孔隙介质圆柱壳 (β =0) 和充黏液
ߘᬩए β=0.20
3.3
孔隙介质圆柱壳 (β = 0.10) 三种模型中超声导波纵
3.2
0 0.02 0.04 0.06 0.08 0.10
向模态相速度频散曲线进行对比，如图 4 所示。根
ᮠဋ/MHz
据表 2、表 3 和表 4 的参数，首先令孔隙介质孔隙度
(a) ঌጫฉ
β =0，将得到的频散曲线与充黏液弹性介质圆柱壳
1.0
的频散曲线相比较 [13] ，从图中可以看到，两种情况
0.9 ߘᬩए β=0.20
0.8 ߘᬩए β=0.10 下(孔隙度β =0充黏液孔隙介质圆柱壳与充黏液弹
ਥጫฉᄱᤴए/(km⋅s -1 ) 0.6 ߘᬩए β=0.05 示根据式(26)孔隙度β =0.10 时得到的充黏液孔隙
性介质圆柱壳) 得到的频散曲线吻合。黑色实线表
0.7
0.5
介质圆柱壳频散曲线，在圆柱壳孔隙度变化时，除了
0.4
0.3
壳中纵向模态相速度曲线存在整体偏移现象，但在
0.2 α 模态的相速度变化不明显，充黏液孔隙介质圆柱
ߘᬩए β=0
0.1 不同的频率下，相速度随孔隙度的变化程度不同。
0 5.0
0.00 0.02 0.04 0.06 0.08 0.10
ᮠဋ/MHz L(0,12)
4.0
(b) ਥጫฉ
2.00 3.0
1.95
ߘᬩए β=0 ᄱᤴए/(km⋅s -1 ) 2.0 L(0,2) L(0,3)
ഷฉᄱᤴए/(km⋅s -1 ) 1.85 ߘᬩए β=0.10 1.0 0 L(0,1) ुভ̮᠏
1.90
ߘᬩए β=0.05
ߘᬩ̮᠏β=0
1.80
α
ߘᬩ̮᠏β=0.10
0
1.75
0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45
1.70
1.65 ߘᬩए β=0.20 ᮠဋ/MHz
图 4 充黏液孔隙圆柱中纵向模态的相速度频散曲线
1.60
0.00 0.02 0.04 0.06 0.08 0.10 Fig. 4 Phase velocity dispersion curves of longi-
ᮠဋ/MHz
tudinal modes in the porous cylinder filled with
(c) ഷฉ
viscous liquid
图 3 孔隙介质中体波相速度随孔隙度和频率变化
2.3 充黏液孔隙介质圆柱壳中导波的频散特性
的频散曲线
分析
Fig. 3 Dispersion curves of the phase velocity of
body waves in a porous medium in function of 根据表 2、表 3 和表 4 的参数，由式 (26) 得到充
frequency for various values of viscosity 黏液孔隙介质圆柱壳的频散曲线 (相速度、群速度)