Page 233 - 《应用声学》2025年第3期

第 44 卷 第 3 期 苏娜娜等： 孔隙度检测长骨骨质疏松的超声导波传播特性 767

频率变小，相速度也在降低，相当于频率轴被压缩 导波由于能量泄漏到黏液中而引起的散射衰减，以
了，导波频散曲线的趋势变化不明显，但各模态的 及孔隙介质的吸收衰减。对于 L(0, 1) 模态，在频段
受影响程度不同。L(0, 1) 模态变化较其他模态多一 0∼0.03 MHz 范围内时，L(0, 1) 模态的衰减较小，可
些，低频段相对高频段变化更大。当孔隙度从 0.05 作为检测模态；而在其他频段，随着频率的增加，
增加到 0.20 时，在频段 0∼0.05 MHz，L(0, 1) 模态的 L(0, 1)模态衰减逐渐明显增大，几乎与频率成正比，
相速度明显下降；而其他模态的相速度仅在截止 不适合检测圆柱壳孔隙含量。同时对于平坦区的
频率附近出现明显下降。孔隙度的变化并不改变 L(0,2∼5) 高阶模态，其衰减也都较小，是可选择的
各模态导波在高频处的相速度，仍接近充黏液孔隙 检测模态，随着频率的增加，其衰减与频率的平方成
介质圆柱壳中内部液体在自由状态下的纵波波速 正比。在同孔隙度下，导波衰减大体上是随着频率
(1.530 km/s)。 的增大而增大。这主要是由于当频率较低时孔隙介
事实上，在低频段 0∼0.03 MHz，从相速度和群 质中孔隙流体的黏滞力起主要作用，衰减较小，而在
速度频散曲线中得出，充黏液孔隙介质圆柱壳中只 高频时，孔隙流体的惯性力起主要作用，衰减较大。
有 2 个纵向模态，且孔隙度与频散曲线之间存在着 在同一频率下，当孔隙度增加时，孔隙介质内的孔隙
明显的关系；而在其他频率段的模态数至少为 3 个。 流体增多，使得导波耗散的能量增大，即导波的衰减
因此，对于选定模态，在一定频率范围内，可以通过 随孔隙度增大而增大 [39] 。这些结果与上节频散分
相速度的变化来判定充黏液孔隙介质圆柱壳的孔 析的结果 (用 L(0, 1) 模态在 0.03 MHz 以下检测；用
隙度，为骨质状况提供一定的理论支持。 L(0, 2∼12)等高阶模态群速度出现最大值的平坦频
段检测) 是一致的。此外，波长随频率的增加而减
2.5 孔隙度对导波衰减的影响
小，高阶导波可能无法在长骨中传播，尤其是在骨质
2.4 节根据频散特性来选择检测充黏液孔隙介
疏松的长骨皮质骨中。因此，低频率、低阶、频散小
质圆柱壳的最佳模态和频率，本节对孔隙介质圆柱
受孔隙度影响较大的导波模态成为长骨皮质骨的
中充黏液时各模态的衰减情况进行分析，与前面所
良好指标。
得结果进行比较。不同孔隙度下充黏液孔隙介质圆
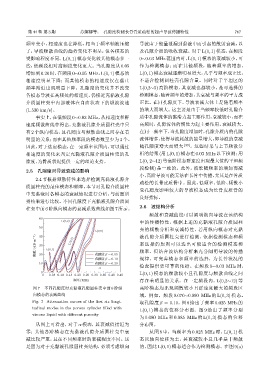
柱壳中前6阶纵向模态的衰减系数曲线如图7所示。 2.6 波结构分析
频散和衰减曲线可以阐明纵向导波在该结构
60
中的传播特性，根据上述的充黏液孔隙介质圆柱
L(0,2)
50 壳的频散分析和衰减特性，若用纵向模态对充黏
L(0,5) 液孔隙介质圆柱壳进行检测，依据检测模态和频
ᛰѓ/(dB⋅m -1 ) 30 L(0,1) L(0,3) 率选择的原则可以选出可能适合的检测模态和
40

频率。但结合波结构分析来充分阐明导波的传播
20
ߘᬩए β=0.05
ߘᬩए β=0.10 规律，可完善模态和频率的选择，为长骨状况的
10 ߘᬩए β=0.20
检查提供更可靠的依据。在频段 0∼0.03 MHz 时，
α
0 L(0, 1) 模态的频散较小且孔隙度与频散曲线之间
0 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45
ᮠဋ/MHz 存在着明显的关系。在一定频段内，L(0,2∼12) 等
图 7 不同孔隙度时充黏液孔隙圆柱壳中前 6 阶纵 高阶模态均出现频散较小且群速度最大的频段区
向模态的衰减曲线 域，例如，频段 0.070∼0.090 MHz 的 L(0, 3) 模态。
Fig. 7 Attenuation curves of the first six longi- 取孔隙度 β = 0.10，图 8 给出了频率 0.025 MHz 的
tudinal modes in the porous cylinder filled with
L(0, 1) 模态的位移分布图。图 9 给出了频率分别
viscous liquid with different porosity
为 0.080 MHz 和 0.085 MHz 的 L(0, 3) 模态的位移
从图上可看出，对于 α 模态，其衰减值接近为 分布图。
零；其他各阶模态在充黏液孔隙介质圆柱壳中衰 从图 8 中，当频率为 0.025 MHz 时，L(0, 1) 模
减比较严重，且在不同频率时的衰减程度不同。这 态以轴向位移为主，其衰减较小且几乎是非频散
是因为对于充黏液孔隙圆柱壳结构，必须考虑纵向 的，因此 L(0, 1) 模态适合作为检测模态。在图 9(a)