Page 104 - 《应用声学》2020年第2期

262 2020 年 3 月

工程应用时，奈奎斯特采样条件下系统采样率 目标回波，处理窗宽设置为两倍信号脉宽，并且处理
通常设置为4 ∼ 10倍的信号上限频率。对于具有较 窗按照50%重叠。奈奎斯特采样时设置系统采样率
高中心频率的系统，若接收信号为带通信号，则常 f s = 136.533 kHz，则处理窗点数 N n = 32768。带
采用带通采样降低系统设计难度。对于下限频率为 通采样时设置系统采样率 f s = 34.133 kHz，则处理
f L 、上限频率为f H 、带宽为B 的带通信号，带通采样 窗点数 N b = 8192。奈奎斯特采样下处理窗点数为
[15] 下采样率需满足 2f H /m 6 f s 6 2f L /(m − 1)， 带通采样下处理窗点数的 4 倍。通过计算，两种采
其中1 6 m 6 ⌊f H /B⌋，符号⌊·⌋为向下取整。 样条件下第 9 个处理窗覆盖完整目标回波，第 8 个
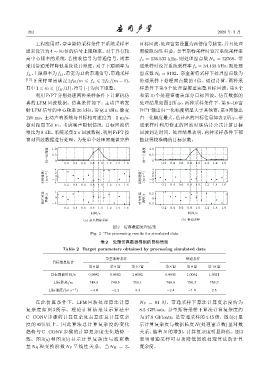
利用 FrFT 分别处理两种采样条件下计算机仿 和第 10 个处理窗覆盖部分目标回波。仿真数据的
真的 LFM 回波数据。仿真条件如下：主动声呐发 处理结果如图 2 所示，两种采样条件下，第 8∼10 窗
射 LFM 信号的中心频率 26 kHz，带宽 3 kHz，脉宽 FrFT输出归一化幅度明显大于其他窗，第9窗输出
120 ms。主动声呐系统与目标相对速度为 −2 m/s， 归一化幅度最大。估计出的目标信息如表2所示，带
相对距离 750 m。考虑噪声限制情况，目标回波信 通采样时利用修正的回波时延估计公式计算目标
噪比为0 dB。系统采集2 s 回波数据，利用FrFT按 回波到达时间。处理结果表明，两种采样条件下都
窗对回波数据进行处理。为使单个处理窗覆盖完整 能获得较准确的目标参数。

ᖂаॆᑵᓖ 1.0 0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 ᖂаॆᑵᓖ 1.0 0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
0.5
0.5

4 2 4 2
ⴞḷ䙏ᓖ/ (mSs -1 ) -2 0 ⴞḷ䙏ᓖ/ (mSs -1 ) -2 0

-4
0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 -4 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
ᑗ޵ᰦᔦ ٿ〫/s 1 0 ᑗ޵ᰦᔦ ٿ〫/s 0.2 0

-1
0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 -0.2 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
௑ᫎ/s ௑ᫎ/s
(a) ݊ݍளྲ᧔ನ (b) ࣜᤰ᧔ನ
图 2 仿真数据处理结果
Fig. 2 The processing results for simulated data
表 2 处理仿真数据得到的目标信息
Table 2 Target parameters obtained by processing simulated data

奈奎斯特采样 带通采样
目标信息估计
第 8 窗 第 9 窗 第 10 窗 第 8 窗 第 9 窗 第 10 窗

目标回波时延/s 0.9985 0.9993 1.0082 0.9995 1.0004 1.0071
目标距离/m 748.9 749.5 756.1 749.6 750.3 755.3
目标速度/(m·s −1 ) −3.0 −2.2 3.3 −2.4 −1.9 2.5

在此仿真条件下，LFM 回波处理算法计算 N P = 81 时，带通采样下算法计算复杂度约为
复杂度如图 3 所示。理论计算结果显示算法中 8.5 GFloats，奈奎斯特采样下算法计算复杂度约
C_CONV 步骤的计算复杂度占算法总计算复杂 为 37.8 GFloats，是带通采样的 4.45 倍。图 3(c) 显
度的 95% 以上，因此算法总计算复杂度的变化 示计算复杂度与数据长度 N(处理窗点数) 呈对数
趋势与 C_CONV 步骤的计算复杂度变化趋势一 关系，随着 N 的增加，计算复杂度明显降低。图 3
致。 图 3(a) 和图 3(b) 显示计算复杂度与波束数 表明带通采样可显著降低回波处理算法的计算
量 N B 和变换阶数 N P 呈线性关系。当 N B = 3、 复杂度。