Page 105 - 《应用声学》2020年第2期

第 39 卷 第 2 期 詹飞等： 水下回波处理中分数阶傅里叶变换的带通采样实现方法 263

√
300 式 (3) 中，S = t 0 /f s 为量纲归一化尺度因子 [16] 。
M/֒ N/8192֒ N P/ 最佳投影 ˆu 0 对应的时延为处理窗内 LFM回波时延
๏ག୲ͻ஝GFloats / 200 ࣜᤰ᧔ನ֒ N b/N 偏移量， f 0 t 0 ˆ u 0 csc ˆα 0
250
݊ݍளྲ᧔ನ֒ N n /N
150
ˆ
100
k 0 S
k 0
50 ut 0 = ˆ + 2 − ˆ , ˆα 0 ̸= kπ, (4)
0 式 (4) 成立的基础是量纲归一化时用处理窗宽 t 0
5 10 15 20
代替信号脉宽 ∆t，用系统采样率 f s 代替信号带
ฉౌ஝᧚N B
(a) ฉౌ஝᧚N B ԫӑ
宽 ∆f 得到尺度因子 S，并且系统采样率 f s 满足
300
M/֒ N=8192֒ N B / 奈奎斯特采样定理。此时信号的能量限定在以
250
๏ག୲ͻ஝GFloats / 200 ࣜᤰ᧔ನ֒ N b /N ∆x = √ t 0 · f s = √ N。当系统采样率 f s 不满足
݊ݍளྲ᧔ನ֒ N n /N
， 其中
原点为中心、 以 ∆x/2 为半径的圆内
[17]
150
奈奎斯特采样时，即带通采样下无法利用该公式
100
50 计算出正确的目标回波时延。为解决此问题，本
文对该公式进行了修正。带通采样条件下，经过
0
10 20 30 40 50 60 70 80
量纲归一化后信号的能量被限制在时频平面上以
ԫ૱᫽஝ N P
(b) ԫ૱᫽஝N P ԫӑ −⌊m/2⌋∆x为中心、以∆x/2为半径的圆内。图4 显
示了 m = 2 时 FrFT 示意图，信号的瞬时频率函数
๏ག୲ͻ஝/GFloats 100 ࣜᤰ᧔ನ֒ N b /N 上的投影为 [ ( t 0 ) ] (5)
M/֒ N B /֒ N P /
150
与新坐标系频域轴的交点在旋转了 −α 角度的 u 轴
݊ݍளྲ᧔ನ֒ N n /N
50

0 u = f 0 S − k 0 S τ − 2 − ∆x sin α.
512 1024 2048 4096 8192 16384 32768 t 
t 
֓֓ Dt ֓
஝૶඀᫂एN  
(c) ஝૶᫂एN ԫӑ
τ f 0 f c k 0
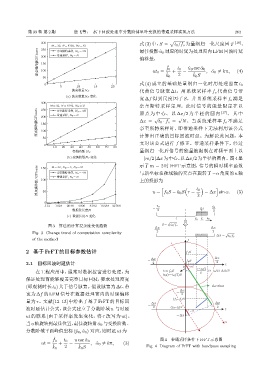
图 3 算法的计算复杂度变化趋势 Dx S/ t 0⊳f s Dx
֓֓ ֓
Fig. 3 Change trend of computation complexity  
Dx/ t 0Sf s
of the method f
2 基于FrFT的目标参数估计 f 1 S
Dx
Dx
֓֓ f 0 S ֓

2.1 目标回波时延估计  t
0 −α
τ֓t  ⊳
在工程应用中，通常对数据按窗进行处理，为 b/f  S֓ S ↼τ֓t  ⊳⇁Dt↽⊳S
k 0 ↼τ֓t  ⊳↽S
保证处理窗能够覆盖完整目标回波，要求处理窗宽
(即观测时长 t 0 ) 大于信号脉宽。假设脉宽为 ∆t、带 DxSsinα
Dx
宽为 ∆f 的 LFM 信号在数据处理窗内的时延偏移 ֓֓

量为 τ。文献 [12–13] 中给出了基于 FrFT 的目标回 ↼f 1 ֓f s ↽S Dx
Dx
֓֓ ֓
波时延估计公式，该公式建立了分数阶域 u 与时延  ↼f 0 ֓f s ↽S  t
−α
ut 的联系 (由于采样率发生变化，将 τ 改写为 ut)。 -Dx
当u轴旋转到最佳位置，最佳旋转角 ˆα 0 与变换阶数- u
分数阶域平面峰值坐标(ˆp 0 , ˆu 0 ) 对应，则时延ut为
ˆ 带通采样条件下 FrFT 示意图
f 0 t 0 u csc ˆα 0 图 4
ut = + − , ˆα 0 ̸= kπ, (3)
ˆ 2 ˆ Fig. 4 Diagram of FrFT with bandpass sampling
k 0 k 0 S