Page 147 - 《应用声学》2020年第2期

第 39 卷 第 2 期 王文文等： 基于多基因遗传规划的储层岩石静态模量预测 305

30
25
20
E sta /GPa 15

10
5
0 ࠄᰎ MGGP ጳভલՌ
-5
5 10 15 20
No.
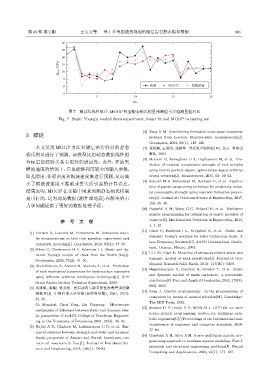
图 7 测试集线性拟合、MGGP 模型静态杨氏模量预测值与实验测量值对比
Fig. 7 Static Young’s moduli from experiment, linear fit and MGGP in testing set

[6] Tang X M. Determining formation shear-wave transverse
5 结论 isotropy from borehole Stoneley-wave measurements[J].
Geophysics, 2003, 68(1): 118–126.
本文采用 MGGP 方法对储层砂岩样品的静态 [7] 张海澜, 王秀明, 张碧星. 井孔的声场和波 [M]. 北京: 科学出
杨氏模量进行了预测。该模型比用动态数据线性拟 版社, 2004.
[8] Momeni E, Armaghani D J, Hajihassani M, et al. Pre-
合标定的经验关系有更好的适应性。此外，在缺失
diction of uniaxial compressive strength of rock samples
横波速度的情况下，它也能够利用较少的输入参数， using hybrid particle swarm optimization-based artificial
即孔隙度、体积密度和纵波速度来进行预测，从而减 neural networks[J]. Measurement, 2015, 60: 50–63.
[9] Salooki M K, Esfandyari M, Rabbani E, et al. Applica-
小了横波波速度不准确或丢失所引起的计算误差。
tion of genetic programing technique for predicting uniax-
结果表明，MGGP 在实验中用来预测静态杨氏模量 ial compressive strength using reservoir formation proper-
是可行的，这为现场数据 (测井或地震) 在解决岩石 ties[J]. Journal of Petroleum Science & Engineering, 2017,
159: 35–48
力学问题提供了更好的数据处理手段。
[10] Bayazidi A M, Wang G G, Bolandi H, et al. Multigene
genetic programming for estimation of elastic modulus of
参 考 文 献 concrete[J]. Mathematical Problems in Engineering, 2014,
1: 1–10.
[11] Olsen C, Fabricius I L, Krogsboll A, et al. Static and
[1] Yurikov A, Lebedev M, Pervukhina M. Ultrasonic veloc-
dynamic Young’s modulus for lower Cretaceous chalk. A
ity measurements on thin rock samples: experiment and
Low Frequency Scenario[C]. AAPG International Confer-
numerical modeling[J]. Geophysics, 2018, 83(2): 47–56.
ence. Cancun, Mexico, 2004.
[2] Olsen C, Christensen H F, Fabricius I L. Static and dy-
[12] Li L M, Fjaer E. Modeling of stress-dependent static and
namic Young’s moduli of chalk from the North Sea[J].
dynamic moduli of weak sandstones[J]. Journal of Geo-
Geophysics, 2008, 73(2): 41–50.
physical Research-Solid Earth, 2012: 117(B5): 5206.
[3] Abdulraheem A, Ahmed M, Vantala A, et al. Prediction
[13] Hassanzadegan A, Guerizec R, Reinsch T, et al. Static
of rock mechanical parameters for hydrocarbon reservoirs
and dynamic moduli of malm carbonate: a poroelastic
using different artificial intelligence techniques[C]. SPE
correlation[J]. Pure and Applied Geophysics, 2016, 173(8):
Saudi Arabia Section Technical Symposium, 2009.
2841–2855.
[4] 葛洪魁, 陈颙, 林英松. 岩石动态与静态弹性参数差别的微
[14] Koza J. Genetic programming: on the programming of
观机理 [J]. 中国石油大学学报 (自然科学版), 2001, 25(4):
computers by means of natural selection[M]. Cambridge:
34–36.
The MIT Press, 1992.
Ge Hongkui, Chen Yong, Lin Yingsong. Microscopic
[15] Searson D P, Leahy D E, Willis M J. GPTIPS: an open
mechanism of difference between static and dynamic elas-
source genetic programming toolbox for multigene sym-
tic parameters of rock[J]. College of Petroleum Engineer-
bolic regression[C]//Proceedings of the International mul-
ing in the University of Petroleum, 2001, 25(4): 34–36.
ticonference of engineers and computer scientists, 2010:
[5] Najibi A R, Ghafoori M, Lashkaripour G R, et al. Em-
77–80.
pirical relations between strength and static and dynamic
[16] Gandomi A H, Alavi A H. A new multi-gene genetic pro-
elastic properties of Asmari and Sarvak limestones, two
gramming approach to nonlinear system modeling. Part I:
main oil reservoirs in Iran[J]. Journal of Petroleum Sci-
materials and structural engineering problems[J]. Neural
ence and Engineering, 2015, 126(1): 78–82.
Computing and Applications, 2012, 21(1): 171–187.