Page 81 - 《应用声学》2020年第2期

第 39 卷 第 2 期 刘凯悦等： 水下对空中声源的运动参数估计 239

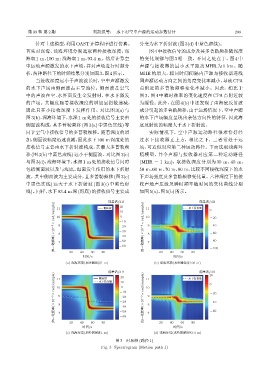
针对上述模型，利用OAST计算程序进行仿真。 分变为水下折射波(图3(d)中蓝色虚线)。
首先对深海、浅海环境分别选取两种接收深度，深 图4中接收信号的成分及其多普勒频移随深度
海取 1 m、100 m；浅海取 1 m、93.4 m。然后计算空 的变化规律与图 3 相一致。不同之处在于，图 4 中
中运动声源激发的水下声场，并对声场进行时频分 声源与接收器的最小水平距离 MHR 为 1 km。随
析，两种路径下的时频结果分别如图3、图4所示。 MHR 的增大，相同时间间隔内声源与接收器连线
当接收深度远小于声波波长时，空中声源激发 同声源运动方向之间的角度变化率减小，导致CPA
的水下声场由侧面波占主导地位。侧面波是空气 点附近的多普勒频移变化率减小。因此，相比于
中的声波在空 -水界面发生全发射时，在水下激发 图 3，图 4 中瞬时频率的变化速度在 CPA 点附近较
的声场。其幅度随着接收深度的增加呈指数递减， 为缓慢。此外，在图 4(b) 中还发现了由海底反射波
因此只在小接收深度下发挥作用。对比图 3(a) 与 成分引起的多普勒频移，由于远场情况下，空中声源
图 3(b)，深海环境下，水深1 m处的接收信号主要由 的水下声场幅度呈现出余弦方向性的特征，因此海
侧面波构成，其多普勒频移 (图 3(a) 中黑色实线) 等 底反射波的幅度大于水下折射波。
同于空气中接收信号的多普勒频移。随着深度的增 实际情况下，空中声源运动路径很难恰好经
加，侧面波幅度迅速衰减，因此水下100 m深度处的 过水下接收器正上方，相比之下，二者常处于远
接收信号主要由水下折射波构成，其最大多普勒频 场，可近似对应第二种运动路径。下面选取浅海环
移(图3(b)中蓝色虚线) 远小于侧面波。对比图 3(c) 境模型，并令声源与接收器对应第二种运动路径
与图3(d)，浅海环境下，水深1 m处的接收信号同时 (MHR = 1 km)，取接收深度分别为 30 m、40 m、
包括侧面波以及与海底、海面发生作用的水下折射 50 m、60 m、70 m、80 m，比较不同接收深度下的水
波。其中侧面波为主要成分，且多普勒频移 (图 3(c) 下声场强度及多普勒频移变化量。六种深度下的接
中黑色实线) 远大于水下折射波 (图 3(c) 中蓝色虚 收声场声压级及瞬时频率随时间的变化曲线分别
线)。同样，水下93.4 m深(海底)的接收信号主要成 如图5(a)、图5(b)所示。

ᑟ᧚៨/dB 11 ඵʾઉ࠱ฉ 0
ᑟ᧚៨/dB
ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -10 ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -20
20
Ο᭧ฉ
11
10
0
-40
-20
-30
-60
-40
-80
-50
7
60
40
20
௑ᫎ/s 60 80 -60 7 20 40 ௑ᫎ/s 80 -100
(a) ງ๒ဗܒ(ඵզ٨ງए1 m) (b) ງ๒ဗܒ(ඵզ٨ງए100 m)
ᑟ᧚៨/dB
ᑟ᧚៨/dB 11 ඵʾઉ࠱ฉ 20
ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -10 ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -20
20
Ο᭧ฉ
11
ඵʾઉ࠱ฉ
10
0
0
-20
-30
-40
-40
-60
-50
7
40
20
60
௑ᫎ/s 60 80 -60 7 20 40 ௑ᫎ/s 80
(c) ู๒ဗܒ(ඵզ٨ງए1 m) (d) ู๒ဗܒ(ඵզ٨ງए93.4 m)
图 3 时频图 (路径 1)
Fig. 3 Spectrogram (Motion path 1)