Page 82 - 《应用声学》2020年第2期

240 2020 年 3 月

ᑟ᧚៨/dB 11 ๒अԦ࠱ฉ -20
ᑟ᧚៨/dB
ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -10 ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -40
Ο᭧ฉ
11
0
ඵʾઉ࠱ฉ
-30
-20
-50
-30
-60
-40
-70
-50
-80
-60
7
-100
20
40
௑ᫎ/s 60 80 -70 7 20 40 ௑ᫎ/s 60 80 -90
(a) ງ๒ဗܒ(ඵզ٨ງए1 m) (b) ງ๒ဗܒ(ඵզ٨ງए100 m)
ᑟ᧚៨/dB
ᑟ᧚៨/dB 11 ඵʾઉ࠱ฉ -10
ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -10 ॆʷӑᮠဋ(T10 -3 p rad/sample) 10 9 8 -20
Ο᭧ฉ
11
0
ඵʾઉ࠱ฉ
-20
-30
-30
-40
-40
-50
-50
-60
-60
-70
7
20
40
௑ᫎ/s 60 80 -70 7 20 40 ௑ᫎ/s 60 80 -80
(c) ู๒ဗܒ(ඵզ٨ງए1 m) (d) ู๒ဗܒ(ඵզ٨ງए93.4 m)
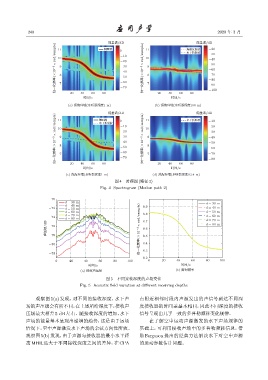
图 4 时频图 (路径 2)
Fig. 4 Spectrogram (Motion path 2)
-70
d=30 m d=30 m
d=40 m
-72 d=50 m 8.9 d=40 m
d=60 m d=50 m
d=70 m 8.8 d=60 m
-74
d=80 m 8.7 d=70 m
ܦԍጟ/dB -76 ॆʷӑᮠဋ(T10 -3 p rad/sample) 8.6 d=80 m
-78
8.5
-80 8.4
-82 8.3
8.2
0 20 40 60 80 100 0 20 40 60 80 100
௑ᫎ/s ௑ᫎ/s
(a) ଌஆܦԍጟ (b) ᅯ௑ᮠဋ

图 5 不同接收深度的声场变化
Fig. 5 Acoustic field variation at different receiving depths

观察图 5(a) 发现，对不同的接收深度，水下声 点附近相邻时段内声源发出的声信号到达不同深
场的声压级会有所不同，在上述所给深度下，接收声 度接收器的时间差基本相同，因此不同深度的接收
压级最大相差 5 dB 左右。随接收深度的增加，水下 信号呈现出几乎一致的多普勒频移变化规律。
声场的能量基本呈现出递增的趋势，这是由于远场 在了解空中运动声源激发的水下声场规律的
情况下，空中声源激发水下声场的余弦方向性所致。 基础上，可利用接收声场中的多普勒频移信息，借
观察图 5(b) 发现，由于声源与接收器的最小水平距 助 Ferguson 提出的经典方法解决水下对空中声源
离 MHR 远大于不同接收深度之间的差异，在 CPA 的运动参数估计问题。